Questão Fundamentos da matemática elementar vol 9

por Serg.io Qua 20 Nov 2019, 13:15

(COMBITEC-COMBIMED-75) Dois quadrados interceptam-se conforme a figura, sendo que o qua- drado maior, de área A, lem um de seus vértices no centro do outro quadrado, de área a. A área da su- perficie tracejada é:

a) A+a/2
b)(a√3)/4
c)(A√3+a)/4
d) a/4
e) √(A•a)

Gabarito : d

Questão Fundamentos da matemática elementar vol 9 Img-2012

por **Elcioschin** Qua 20 Nov 2019, 14:38

Algumas dicas na figura.

Depois basta calcular áreas de polígonos (triângulos, quadriláteros, etc.)

Questão Fundamentos da matemática elementar vol 9 Quadra15

por **Rory Gilmore** Qua 20 Nov 2019, 14:44

A área hachurada não é igual a a/4 pois a área do triângulo em que ela está contida é igual a/4. Entendo que a questão queira a área de interseção entre os dois quadrados e para calcular tal área temos:

I) Seja o ângulo BOF = x, logo o ângulo DOF = 90 - x.

II) De (I) temos que o ângulo DOE = 90 - (90 - x) = x, ou seja, o ângulo BOF é igual ao ângulo DOE.

II) Pelo caso ALA os triângulos EOD E FOB são congruentes.

III) Em decorrência de (II) a área de interseção é equivalente a área do triângulo DOB, logo:
Lado do quadrado = √a
altura do Triângulo DOB = √a/2
Área = √a.(√a/2) : 2 = a/4

Questão Fundamentos da matemática elementar vol 9 Sem_tz22

por **Ashitaka** Qua 20 Nov 2019, 15:00

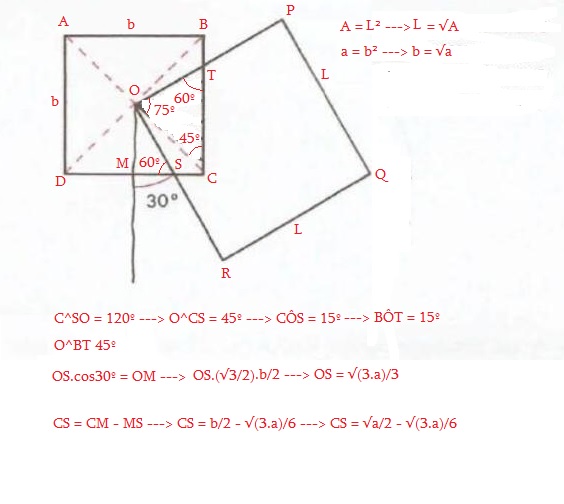
Seja p o lado do quadrado menor. Seja x a base do triângulo tracejado sobre o lado do quadrado menor. O lado superior do quadrado maior que parte do centro do menor tem uma inclinação de 30 graus com a horizontal.

tg(30) = (x-p/2)/(p/2)
1/√3 = (2x - p)/p
p(1 + √3) = 2x√3
x = (√3 + 1)p/(2√3)

Mas p² = a e a área do triângulo é x*(p/2)/2 = xp/4, logo:
Área = (√3 + 1)p²/(8√3) = (√3 + 1)a²/(8√3) = (3 + √3)a/24

Nitidamente, a resposta não tem como ser a/4, pois esta é a área compreendida entre duas linhas tracejadas vermelhas e, como é possível ver, os lados do quadrado maior não estão sobre elas.

por **Ashitaka** Qua 20 Nov 2019, 15:08

Rory Gilmore escreveu:A área hachurada não é igual a a/4 pois a área do triângulo em que ela está contida é igual a/4. Entendo que a questão queira a área de interseção entre os dois quadrados e para calcular tal área temos:

I) Seja o ângulo BOF = x, logo o ângulo DOF = 90 - x.

II) De (I) temos que o ângulo DOE = 90 - (90 - x) = x, ou seja, o ângulo BOF é igual ao ângulo DOE.

II) Pelo caso ALA os triângulos EOD E FOB são congruentes.

III) Em decorrência de (II) a área de interseção é equivalente a área do triângulo DOB, logo:
Lado do quadrado = √a
altura do Triângulo DOB = √a/2
Área = √a.(√a/2) : 2 = a/4

Pela configração dos quadrados, a área de intersecção deles sempre será a/4, independentemente da rotação do maior.

por **Rory Gilmore** Qua 20 Nov 2019, 15:26

Ashitaka escreveu:
Rory Gilmore escreveu:A área hachurada não é igual a a/4 pois a área do triângulo em que ela está contida é igual a/4. Entendo que a questão queira a área de interseção entre os dois quadrados e para calcular tal área temos:

I) Seja o ângulo BOF = x, logo o ângulo DOF = 90 - x.

II) De (I) temos que o ângulo DOE = 90 - (90 - x) = x, ou seja, o ângulo BOF é igual ao ângulo DOE.

II) Pelo caso ALA os triângulos EOD E FOB são congruentes.

III) Em decorrência de (II) a área de interseção é equivalente a área do triângulo DOB, logo:
Lado do quadrado = √a
altura do Triângulo DOB = √a/2
Área = √a.(√a/2) : 2 = a/4

Pela configração dos quadrados, a área de intersecção deles sempre será a/4, independentemente da rotação do maior.

Bem observado.