Inequação do segundo grau

por viniciuscz Sex 11 Out 2019, 16:40

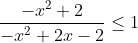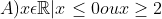
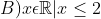
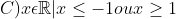
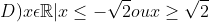
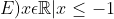
O conjunto de todos os valores reais de x que satisfazem a desigualdade $Inequação do segundo grau Gif$ é:

$Inequação do segundo grau Gif$
$Inequação do segundo grau Gif$
$Inequação do segundo grau Gif$
$Inequação do segundo grau Gif$
$Inequação do segundo grau Gif$

por Motumbus brasiliensis Sex 11 Out 2019, 17:13

Tem certeza que é essa a equação? Quebrei a cabeça aqui e não saiu nada. Nenhuma das respostas dão certo, além de que a equação do denominador dá raízes complexas, então não dá pra fazer o quadro de sinais, ai não tem como achar o intervalo ao qual pertence o x...

Se não for o caso, que alguém responda ai

por **Elcioschin** Sex 11 Out 2019, 17:20

....- x² + 2 .......................- x² + 2 - (- x² + 2.x - 2) ................. - 2.(x - 2)
---------------- - 1 ≤ 0 ---> ------------------------------ ≤ 0 ---> ------------------ ≤ 0
- x² + 2.x - 2 .......................... - (x² - 2.x + 2) .................... - (x² - 2.x + 2)

..,2.(x - 2)
-------------- ≤ 0
x² - 2x + 2

A função do denominador é uma parábola com a concavidade voltada para cima e tem raízes complexas; isto significa que ela é sempre positiva (está acima do eixo x)

Logo, o sinal da expressão depende apenas do sinal da função do numerador, que tem raiz x = 2

Solução --> x ≤ 2 ---> B

por Motumbus brasiliensis Sex 11 Out 2019, 17:23

Nossa, é mesmo!! Que deslize. Finge que eu não postei nd hehehe

por viniciuscz Sex 11 Out 2019, 17:50

Elcioschin escreveu:....- x² + 2 .......................- x² + 2 - (- x² + 2.x - 2) .......
---------------- - 1 ≤ 0 ---> ------------------------------ ≤ 0
- x² + 2.x - 2 .......................... - (x² - 2.x + 2) .............

Por que o - (x² - 2.x + 2) ficou no numerador?