PiR2
Gostaria de reagir a esta mensagem? Crie uma conta em poucos cliques ou inicie sessão para continuar.
PiR2

O fórum do Euclides - Destinado a estudantes

  • Início
  • Fundamentos da Matemática Elementar T3Ri1xW
  • Extras
  • Entrar
  • Registrar
  • Últimas imagens

Fundamentos da Matemática Elementar

2 participantes

PiR2 :: Matemática :: Álgebra

Ir para baixo

Fundamentos da Matemática Elementar Empty Fundamentos da Matemática Elementar

Mensagem por Luciano Augusto Qui 19 Set 2019, 14:06

Considere o conjunto A = {y ∈ Ζ tal que ΙyΙ < 4}. Responda:
a) Qual o número de equações do tipo x² + 2mx + n = 0, com m ∈ A e n ∈ A?
b) Dentre as equações obtidas no item a, quantas têm raízes reais e distintas?
c) Dentre as equações com raízes reais e distintas, quantas têm raízes positivas?

Gabarito: a) 49 b) 30 c) 6

Eu consegui fazer a letra a) porem a letra b) cheguei no valor de 39 equações e no Gabarito esta que são 30 equações, e claro que a letra c) tambem não fiz pois ela depende do resultado da letra b)

Essa é a resolução que eu tive na letra b)
Para ter raizes reais e distintas o delta tem de ser maior que zero
∆=b²-4*a*c --> ∆=(2m)²-4*1*n --> ∆=4m²-4n --> ∆=4(m²-n) --> 4(m²-n)>0 --> m²-n>0 --> m²>n


Feito isso tive 39 equações que atendiam a m²>n.


Desde já agradeço!
Luciano Augusto
Luciano Augusto
Recebeu o sabre de luz
Recebeu o sabre de luz

Mensagens : 133
Data de inscrição : 21/07/2019
Idade : 23
Localização : Mogi das Cruzes - São Paulo - Brasil

Ir para o topo Ir para baixo

Fundamentos da Matemática Elementar Empty Re: Fundamentos da Matemática Elementar

Mensagem por Victor011 Sex 20 Set 2019, 15:13

Você chegou na expressão correta, mas contou os casos de maneira errada. Veja:

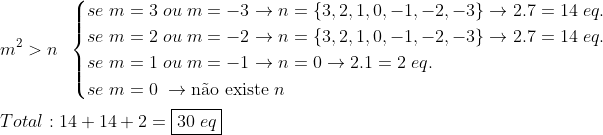
Fundamentos da Matemática Elementar Gif.latex?%5C%5Cm%5E%7B2%7D%3En%5C%3B%5C%3B%5Cbegin%7Bcases%7D%20se%5C%3B%20m%3D3%5C%3Bou%5C%3Bm%3D-3%5Crightarrow%20n%3D%5C%7B3%2C2%2C1%2C0%2C-1%2C-2%2C-3%5C%7D%5Crightarrow2.7%3D14%5C%3Beq.%20%5C%5C%20se%5C%3B%20m%3D2%5C%3Bou%5C%3Bm%3D-2%5Crightarrow%20n%3D%5C%7B3%2C2%2C1%2C0%2C-1%2C-2%2C-3%5C%7D%5Crightarrow2.7%3D14%5C%3Beq.%20%5C%5C%20se%5C%3B%20m%3D1%5C%3Bou%5C%3Bm%3D-1%5Crightarrow%20n%3D0%5Crightarrow2.1%3D2%5C%3Beq

E para fazer a c) você basicamente tem que usar que se as raízes são positivas, então a soma e o produto delas também são, ou seja, n > 0 e m > 0. Ai dá para contar os casos no dedo.
Victor011
Victor011
Fera
Fera

Mensagens : 663
Data de inscrição : 21/10/2015
Idade : 26
Localização : Rio de Janeiro, Brasil

Ir para o topo Ir para baixo

Fundamentos da Matemática Elementar Empty Fundamentos da Matemática Elementar

Mensagem por Luciano Augusto Sex 20 Set 2019, 15:58

Victor011 escreveu:Você chegou na expressão correta, mas contou os casos de maneira errada. Veja:

Fundamentos da Matemática Elementar Gif.latex?%5C%5Cm%5E%7B2%7D%3En%5C%3B%5C%3B%5Cbegin%7Bcases%7D%20se%5C%3B%20m%3D3%5C%3Bou%5C%3Bm%3D-3%5Crightarrow%20n%3D%5C%7B3%2C2%2C1%2C0%2C-1%2C-2%2C-3%5C%7D%5Crightarrow2.7%3D14%5C%3Beq.%20%5C%5C%20se%5C%3B%20m%3D2%5C%3Bou%5C%3Bm%3D-2%5Crightarrow%20n%3D%5C%7B3%2C2%2C1%2C0%2C-1%2C-2%2C-3%5C%7D%5Crightarrow2.7%3D14%5C%3Beq.%20%5C%5C%20se%5C%3B%20m%3D1%5C%3Bou%5C%3Bm%3D-1%5Crightarrow%20n%3D0%5Crightarrow2.1%3D2%5C%3Beq

E para fazer a c) você basicamente tem que usar que se as raízes são positivas, então a soma e o produto delas também são, ou seja, n > 0 e m > 0. Ai dá para contar os casos no dedo.
A primeira e segunda sentença eu entendi, porem a 4 e a 5 eu não entendi;
Pois se for 1 --> 1² = 1 então é maior que -3, -2, -1, e 0 = 4  eq.
Se for -1 --> -1² = 1 então é maior que -3, -2, -1, e 0 = 4  eq.
Se for 0 --> 0² = 0 então é maior que -3, -2, -1 = 3  eq.
juntando com as duas primeiras que são 28 eq. da 39 eq.
Luciano Augusto
Luciano Augusto
Recebeu o sabre de luz
Recebeu o sabre de luz

Mensagens : 133
Data de inscrição : 21/07/2019
Idade : 23
Localização : Mogi das Cruzes - São Paulo - Brasil

Ir para o topo Ir para baixo

Fundamentos da Matemática Elementar Empty Re: Fundamentos da Matemática Elementar

Mensagem por Victor011 Sáb 21 Set 2019, 08:52

Você está correto. Eu estava pensando na equação como m2 > |n| (n em módulo), pois estava preocupado em chegar na resposta. Se a equação for de fato m2 > n, ai são 39 equações mesmo.
Victor011
Victor011
Fera
Fera

Mensagens : 663
Data de inscrição : 21/10/2015
Idade : 26
Localização : Rio de Janeiro, Brasil

Ir para o topo Ir para baixo

Fundamentos da Matemática Elementar Empty Re: Fundamentos da Matemática Elementar

Mensagem por Conteúdo patrocinado


Conteúdo patrocinado


Ir para o topo Ir para baixo

Ir para o topo

- Tópicos semelhantes

PiR2 :: Matemática :: Álgebra

 
Permissões neste sub-fórum
Não podes responder a tópicos