EGMO (geometria)
2 participantes
PiR2 :: Questões Especiais :: Olimpíadas :: Matemática
Página 1 de 1
EGMO (geometria)
por Barbaducki Sáb 14 Set 2019, 15:08
Alguém?
Última edição por Zelderis megantron em Sáb 14 Set 2019, 22:50, editado 1 vez(es)
Barbaducki- Recebeu o sabre de luz
- Mensagens : 119
Data de inscrição : 14/04/2019
Idade : 25
Localização : Rio de Janeiro
Re: EGMO (geometria)
por Elcioschin Sáb 14 Set 2019, 22:22
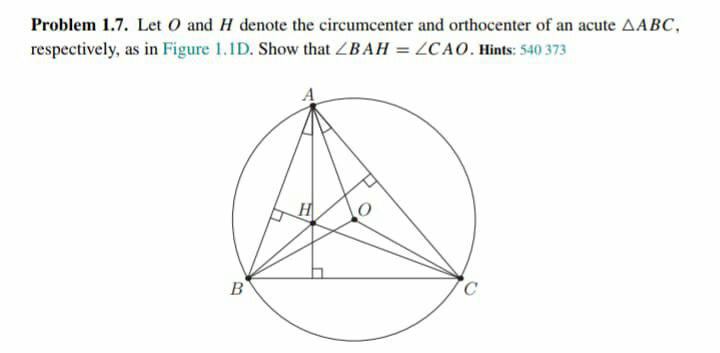
Sejam:
α = OÂB = O^BA
β = O^BC = O^CB
γ = OÂB = O^BA
θ = HÂB ---> OÂH = OÂB - HÂB ---> OÂH = γ - θ
M, N, P os pés das perpendiculares de A, B, C sobre BC, AC, AB
BÂC + A^BC + A^CB = 180º ---> (α + γ) + (β + γ) + (α + β) = 180º ---> α + β + γ = 90º --->
No triângulo retângulo AMB ---> A^BM + MÂB = 90º ---> O^BA + O^BC + θ = 90º ---> γ + β + θ = 90º ---> II
Faça similar no triângulo retângulo BNC ---> III
Com I, II, III ---> θ = α
α = OÂB = O^BA
β = O^BC = O^CB
γ = OÂB = O^BA
θ = HÂB ---> OÂH = OÂB - HÂB ---> OÂH = γ - θ
M, N, P os pés das perpendiculares de A, B, C sobre BC, AC, AB
BÂC + A^BC + A^CB = 180º ---> (α + γ) + (β + γ) + (α + β) = 180º ---> α + β + γ = 90º --->
No triângulo retângulo AMB ---> A^BM + MÂB = 90º ---> O^BA + O^BC + θ = 90º ---> γ + β + θ = 90º ---> II
Faça similar no triângulo retângulo BNC ---> III
Com I, II, III ---> θ = α
Elcioschin- Grande Mestre
- Mensagens : 73176
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Barbaducki- Recebeu o sabre de luz
- Mensagens : 119
Data de inscrição : 14/04/2019
Idade : 25
Localização : Rio de Janeiro
Tópicos semelhantesPiR2 :: Questões Especiais :: Olimpíadas :: Matemática
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
