Circunferência e corda

(MACK-68) A reta 2x+y=0 contém o diâmetro de uma circunferência. Uma reta, que forma ângulo de 45º com a primeira e tem declive positivo, corta a circunferência no ponto (1,1) e determinar sobre a mesma uma corda de comprimento v10 unidades. Estabelecer as equações da segunda reta e da circunferência.


Resposta: Reta: 3x-y-2=0 Circunferência: (x-1/5)²+(y+2/5)²=65/25 e (x+9/5)²+(y-18/5)²=73/5



Achar a equação da reta é tranquilo, qual a ideia para achar as equações da circunferência?

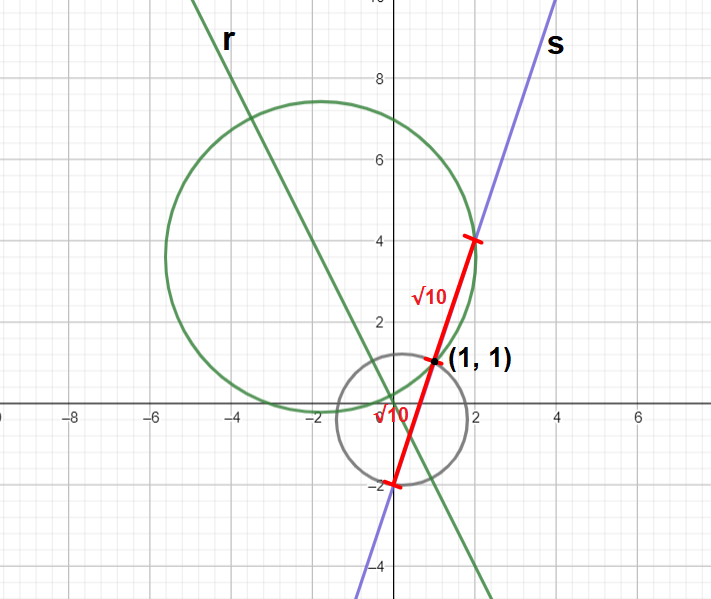
Problema com vários passos, porém bem processual e sem surpresas.

A reta pedida passa por (1, 1). Pela equação rápida da reta:
y - 1 = m(x - 1) --> y = mx - m + 1
Como o problema diz que ela faz 45° com a reta r: y = -2x dada, podemos relacionar seus coef. angulares:
Seja m = -2 = tan(Θ) o coef. angular da reta r, o m' da reta s pedida será tan(Θ±45°), mas para m' ser positivo como pede o enunciado teremos que m' = tan(Θ-45°). Utilizando a fórmula para tangente da diferença conclui-se que m' = 3, logo a reta pedida é s: y = 3x - 2

As circunferências de uma forma genérica são dadas por (x - x꜀)² + (y - y꜀)² = R²
Como o problema diz que a reta r contêm o diâmetro, com certeza ela passa pelos centros, logo podemos utilizá-la para escrever y꜀ em função de x꜀, com o objetivo de diminuir as variáveis no problema:
y꜀ = -2x꜀ --> λ: (x - x꜀)² + (y + 2x꜀)² = R²
Agora utilizamos o ponto (1, 1) dado pertencente à circunferência para obter uma relação:
(1 - x꜀)² + (1 + 2x꜀)² = R² --> 5x꜀² + 2x꜀ + 2 = R² (1)

O próximo passo é utilizar a última informação que faltou, a reta s contêm uma corda de λ com tamanho √10 na qual um dos extremos é o ponto (1, 1) dado. Por distância entre pontos: (x - 1)² + (y - 1)² = 10
Fazendo a interseção desse resultado com a reta s encontramos os pontos (0, -2) e (2, 4), nesse momento fica claro que haverá duas possibilidades para λ no problema.

Substituindo (0, -2) na equação de λ encontramos a relação 5x꜀² - 8x꜀ + 4 = R² (2)
Fazendo o mesmo para (2, 4) encontramos 5x꜀² + 12x꜀ + 20 = R² (3)

Finalmente, basta igualar (2) e depois (3) com (1) para encontrar os x꜀ de λ, utilizando y꜀ = -2x꜀ para encontrar o y꜀ e posteriormente (1) para encontrar os raios, gerando assim as equações de circunferência pedidas.

Visualização no GeoGebra: