Números complexos
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Números complexos
por albert Qua 03 Ago 2011, 15:05
(CONVESU) - Sejam u e v dois complexos tais que u² - v² = 6 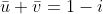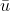e 
. (
e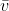 
são os conjugados de u e v).Então u - v é igual a:
a) 1 - i
b) 1 + i
c) 3 + 3i
d) 3 - 3i
e) 2 + 2i
Não estou conseguindo chegar no resultado (para mim, está dando 1 - i). Podem me ajudar? Obrigado!
a) 1 - i
b) 1 + i
c) 3 + 3i
d) 3 - 3i
e) 2 + 2i
Não estou conseguindo chegar no resultado (para mim, está dando 1 - i). Podem me ajudar? Obrigado!
albert- Padawan
- Mensagens : 73
Data de inscrição : 21/03/2011
Idade : 30
Localização : São Paulo, SP, Brasil
Re: Números complexos
por Elcioschin Qua 03 Ago 2011, 16:45
u = a + bi ----> u' = a - bi
v = c + di -----> v' = c - di
u' + v' = 1 - i ----> (a - bi) + (c - di) = 1 - i ----> (a + c) - (b + d)i = 1 - 1
Comparando termo a termo ----> a + c = 1 e b + d = 1
u² - v² = 6 ----> (u + v)*(u - v) = 6 ----> [(a + bi) + (c + di)]*(u - v) = 6 ---->
[(a + c) + (b + d)i]*(u - v) = 6 -----> (1 + i)*(u - v) = 6 ----> u - v = 6/(1 + i) ---->
u - v = 6*(1 - i)/((1 + i)*(1 - i) -----> u - v = 6*(1 - i)/2 ----> u - v = 3 - 3i
v = c + di -----> v' = c - di
u' + v' = 1 - i ----> (a - bi) + (c - di) = 1 - i ----> (a + c) - (b + d)i = 1 - 1
Comparando termo a termo ----> a + c = 1 e b + d = 1
u² - v² = 6 ----> (u + v)*(u - v) = 6 ----> [(a + bi) + (c + di)]*(u - v) = 6 ---->
[(a + c) + (b + d)i]*(u - v) = 6 -----> (1 + i)*(u - v) = 6 ----> u - v = 6/(1 + i) ---->
u - v = 6*(1 - i)/((1 + i)*(1 - i) -----> u - v = 6*(1 - i)/2 ----> u - v = 3 - 3i
Elcioschin- Grande Mestre
- Mensagens : 73182
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Rumo a EsPCEx e lisben gostam desta mensagem
albert- Padawan
- Mensagens : 73
Data de inscrição : 21/03/2011
Idade : 30
Localização : São Paulo, SP, Brasil
Tópicos semelhantesPiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
