Esboce a curva
2 participantes
Página 1 de 1
 Esboce a curva
Esboce a curva
Dada a equação geral x2+y2-2x-6y+6 = 0 faça a redução para a equação canônica e esboce seu gráfico.
Como faço a resolução das questões desse tipo?
Como faço a resolução das questões desse tipo?
Última edição por bsabrunosouza em Dom 14 Jul 2019, 16:22, editado 1 vez(es)
bsabrunosouza- Iniciante
- Mensagens : 5
Data de inscrição : 14/07/2019
Idade : 24
Localização : Aracaju
 Re: Esboce a curva
Re: Esboce a curva
Olá, bem-vindo ao fórum. Recomendo o método de "completar quadrados" , caso não compreenda muito bem, recomendo que pesquise um vídeo sobre. Vamos lá:
O método consiste em tentarmos simplificar a equação dada, por meio da transformação dela em um produto notável, vamos usar uma artimanha, que é adicionarmos dos dois lados da igualdade um termo que nos permite simplificar tudo, veja bem:
x^{2}-2x+y^{2}-6y=-6
x^{2}-2x+1+y^{2}-6y+9=-6+9+1
(x-1)^{2}+(y-3)^{2}=4
"-Mas como eu saberei que número colocar para fazer um produto notável?" Aí vai um bizu:
Lembre-se de que: (X+Y)² = X²+2XY+Y² Certo? Então basta pegarmos o cara que multiplica "x" ou "y", dividirmos por 2 e elevarmos ao quadrado.
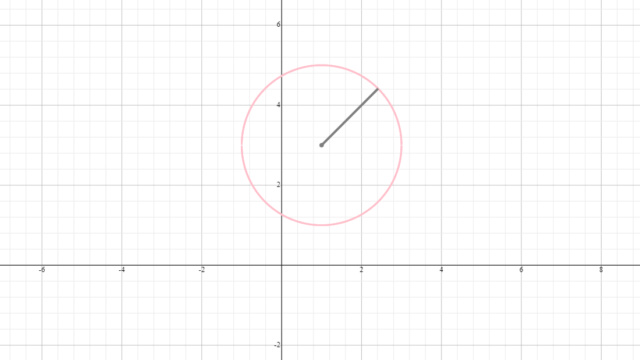
Sabemos agora que se trata de uma circunferência de centro C(1,3) e cujo raio é 2. Logo, o gráfico dessa circunferência será:
O método consiste em tentarmos simplificar a equação dada, por meio da transformação dela em um produto notável, vamos usar uma artimanha, que é adicionarmos dos dois lados da igualdade um termo que nos permite simplificar tudo, veja bem:
Perceba que eu adicionei "1" e "9" dos dois lados, não fazendo diferença alguma na equação
"-Mas como eu saberei que número colocar para fazer um produto notável?" Aí vai um bizu:
Lembre-se de que: (X+Y)² = X²+2XY+Y² Certo? Então basta pegarmos o cara que multiplica "x" ou "y", dividirmos por 2 e elevarmos ao quadrado.
Sabemos agora que se trata de uma circunferência de centro C(1,3) e cujo raio é 2. Logo, o gráfico dessa circunferência será:


SanchesCM- Jedi

- Mensagens : 434
Data de inscrição : 19/09/2016
Idade : 27
Localização : Curitiba, Paraná, Brasil.
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos













