UnB 2° Dia 2016 - Questão 138
2 participantes
Página 1 de 1
 UnB 2° Dia 2016 - Questão 138
UnB 2° Dia 2016 - Questão 138
UnB 2° Dia 2016
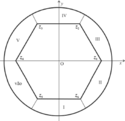
O Museu de Arte Contemporânea de Niterói possui aspectos geométricos interessantes. Um dos pisos contém um salão principal praticamente hexagonal; ao redor desse salão, há cinco galerias e um vão de entrada, que completam um círculo. Nos vértices do hexágono, existem pilastras de sustentação e, em cada uma das diagonais do hexágono, foram construídas vigas de reforço, abaixo do piso. A figura acima apresenta, em um sistema de coordenadas cartesianas ortogonais xOy, uma planta aproximada desse piso, com escala em metros. Cada ponto (x, y) do plano está associado a um número complexo z = x + iy, em que i é a unidade imaginária (i2 = -1). As raízes complexas z1, ..., z6 da equação z6 = 146 identificam a localização das pilastras de sustentação e também os vértices do hexágono que constitui o salão principal; as galerias (identificadas pelos números de I a V, na figura) e o vão de entrada, divididos radialmente, completam a circunferência, definida pela equação |z| = 17. A tabela a seguir apresenta as coordenadas de z1, z2 e z3. As coordenadas de z4, z5 e z6 podem ser obtidas por simetria.
A partir dessas informações, julgue o item.
Abaixo do piso do salão principal, foram construídas 9 vigas de reforço.
a)
Certa
b)
Errada
Uma pessoa comentou na questão que bastava usar a fórmula das diagonais de qualquer polígono, mas sinceramente eu não entendi. Afinal, por que a questão fala tanto de números complexos? E se tem uma viga em cada diagonal da figura (e a figura tem 6 lados), então não deveria ser 6 vigas?
O Museu de Arte Contemporânea de Niterói possui aspectos geométricos interessantes. Um dos pisos contém um salão principal praticamente hexagonal; ao redor desse salão, há cinco galerias e um vão de entrada, que completam um círculo. Nos vértices do hexágono, existem pilastras de sustentação e, em cada uma das diagonais do hexágono, foram construídas vigas de reforço, abaixo do piso. A figura acima apresenta, em um sistema de coordenadas cartesianas ortogonais xOy, uma planta aproximada desse piso, com escala em metros. Cada ponto (x, y) do plano está associado a um número complexo z = x + iy, em que i é a unidade imaginária (i2 = -1). As raízes complexas z1, ..., z6 da equação z6 = 146 identificam a localização das pilastras de sustentação e também os vértices do hexágono que constitui o salão principal; as galerias (identificadas pelos números de I a V, na figura) e o vão de entrada, divididos radialmente, completam a circunferência, definida pela equação |z| = 17. A tabela a seguir apresenta as coordenadas de z1, z2 e z3. As coordenadas de z4, z5 e z6 podem ser obtidas por simetria.
A partir dessas informações, julgue o item.
Abaixo do piso do salão principal, foram construídas 9 vigas de reforço.
a)
Certa
b)
Errada
Uma pessoa comentou na questão que bastava usar a fórmula das diagonais de qualquer polígono, mas sinceramente eu não entendi. Afinal, por que a questão fala tanto de números complexos? E se tem uma viga em cada diagonal da figura (e a figura tem 6 lados), então não deveria ser 6 vigas?
marcelofarias501- Iniciante
- Mensagens : 26
Data de inscrição : 26/06/2019
Idade : 27
Localização : Fortaleza, Ceará, Brasil
marcelofarias501- Iniciante
- Mensagens : 26
Data de inscrição : 26/06/2019
Idade : 27
Localização : Fortaleza, Ceará, Brasil
 Re: UnB 2° Dia 2016 - Questão 138
Re: UnB 2° Dia 2016 - Questão 138
O hexágono possui apenas 3 diagonais: z1z5, z2z4 e z3z6.
Assim, não são 6 vigas como vc escreveu, nem 9 como afirma o item.
Assim, não são 6 vigas como vc escreveu, nem 9 como afirma o item.

Elcioschin- Grande Mestre

- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Tópicos semelhantes
Tópicos semelhantes» ITA 2016 questão 3
» ITA 2016 questão 6
» Questão FGV RJ 2016
» QUESTÃO CMBH 2016 1º ANO
» UNB 2016, questão de sistema
» ITA 2016 questão 6
» Questão FGV RJ 2016
» QUESTÃO CMBH 2016 1º ANO
» UNB 2016, questão de sistema
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos