Espcex 2018, Geometria plana triangulo

por Aprendiz de cadete Seg 31 Dez 2018, 15:59

Em um triângulo ABC, BC=12 cm e a mediana relativa a esse lado mede 6 cm. Sabendo-se que a mediana relativa ao lado AB mede 9 cm, qual a área desse triângulo?

Espcex 2018, Geometria plana triangulo Forum_11

por **Mateus Meireles** Seg 31 Dez 2018, 16:39

Você já ouviu falar do "Teorema do k" ?

por Aprendiz de cadete Seg 31 Dez 2018, 16:45

Mateus Meireles escreveu:Você já ouviu falar do "Teorema do k" ?

Não, pesquisei aqui e não achei nada, do que se trata?

por **Mateus Meireles** Seg 31 Dez 2018, 17:55

Na verdade, não precisa, agora que fui ver que é baricentro

Espcex 2018, Geometria plana triangulo Pir2f11

O baricentro (ponto de encontro das medianas) divide o triângulo ABC em 6 triângulos menores de mesma área.

Por Heron, temos que a área de um deles vale

\begin{align*}

A = \sqrt{(p(p-a)(p-b)(p-c)}\, =\, & \sqrt{(7)(7-2)(7-6)(7-6)} \\
=\, & \sqrt{35}

\end{align*}

Como o triângulo ABC é formado por 6 triângulos menores, temos que a área pedida vale 6\sqrt{35}

por **paulinoStarkiller** Seg 31 Dez 2018, 18:06

Desculpa por me intrometer, mas, Mateus, poderia enunciar qual seria esse "teorema do k"?

Obg Smile

por Aprendiz de cadete Seg 31 Dez 2018, 18:31

Sim, muito obrigado Matheus, mas pode nos explicar o tal "teorema do k"?

por **Mateus Meireles** Ter 01 Jan 2019, 14:57

Não é bem um teorema, por isso que eu coloquei entre aspas, é mais uma relação entre segmentos de pontos interiores a triângulos relacionado com áreas

Vejam o vídeo a partir de 1:04:00 (inclusive ele mostra o fato que eu usei nesse problema, que o baricentro divide o triângulo ABC em 6 triângulos menores de mesma área)

O que vocês querem ver fica em 1:11:10. No final do vídeo ele sugere um problema bem parecido com esse, mas é fornecido o valor das medianas, e não do lado como ocorre aqui

Abraço e feliz ano novo a todos!!

por GBRezende Seg 06 maio 2019, 23:15

Bati a cabeça mais do que devia nessa questão, mas vou mandar aqui a resolução que cheguei que é um pouco mais simples que a do colega, só pra ninguém pensar que seria obrigatório conhecer este teorema para resolver a questão.

Veja que a mediana divide o triângulo em 2 triângulos isósceles. Nomeando os ângulos e trabalhando, é fácil concluir que o triângulo dado é retângulo.

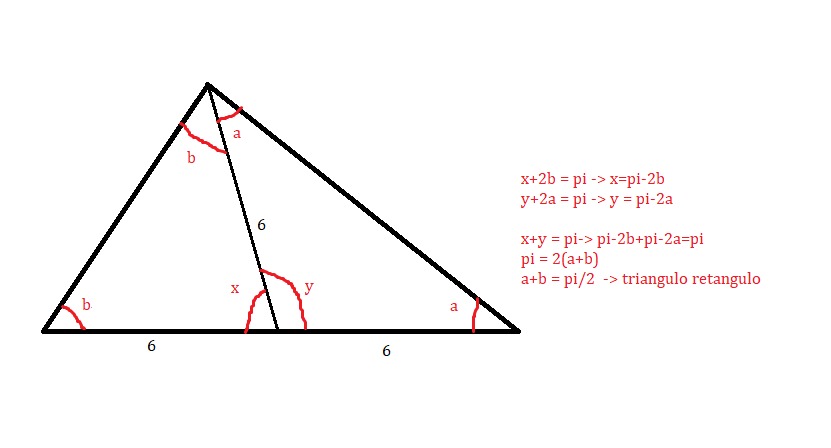
Espcex 2018, Geometria plana triangulo Whatsa14

Agora podemos desenhar a mediana de comprimento 9, e aplicando 2 teoremas de pitágoras, chegará em um sistema para x e y, e bastará resolve-lo para achar os lados desejados.