Sistemas de Equações de Ordem Superiores
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Sistemas de Equações de Ordem Superiores
por ALEXANDRE RESENDE DE SOUZ Dom 21 Out 2018, 11:42
Bom dia! Estou resolvendo a prova do último concurso da cidade de Maricá, porém, travei na questão 43. Vamos lá!
COSEAC/UFF
Questão 43
Considere a função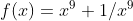
com domínio D={
} e contradomínio 
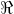. É verdadeiro afirmar que:
(A)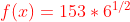
(B)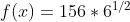
(C)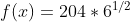
(D)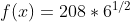
(E)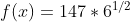
Gabarito: letra (A)
Obrigado e um ótimo domingo.
COSEAC/UFF
Questão 43
Considere a função
(A)
(B)
(C)
(D)
(E)
Gabarito: letra (A)
Obrigado e um ótimo domingo.
ALEXANDRE RESENDE DE SOUZ- Padawan
- Mensagens : 99
Data de inscrição : 27/10/2010
Idade : 45
Localização : Rio Bonito, Rio de Janeiro, Brasil -
Re: Sistemas de Equações de Ordem Superiores
por Elcioschin Dom 21 Out 2018, 14:09
x² + 1/x² = 4
a) (x + 1/x)² = (x² + 1/x²) + 2 ---> (x + 1/x)² = 4 + 2 ---> x + 1/x = √6 = 61/2 ---> I
b) (x + 1/x)³ = x³ + 1/x³ + 3.(x + 1/x) ---> (√6)³ = x³ + 1/x³ + 3.√6 ---> x³ + 1/x³ = 3.√6 ---> II
c) (x² + 1/x²)² = x4 + 1/x4 + 2 ---> 4² = x4 + 1/x4 + 2 ---> x4 + 1/x4 = 14 ---> III
d) (x + 1/x)5 = x5 + 5.(x3 + 1/x3) + 10.(x + 1/x) + 1/x5 ---> (√6)5 = x5 + 5.(3.√6) + 10.√6 --->
x5 + 1/x5 = 11.√6 ---> IV
e) Faça similar para (x + 1/x)7 e calcule x7 + 1/x7
f) (x4 + 1/x4)² = x8 + 1/x8 + 2 ---> 14² = x8 + 1/x8 + 2 ---> x8 + 1/x8 = 194 ---> III
x9 + 1/x9 = (x8 + 1/x8).(x + 1/x) - x7 - 1/x7
a) (x + 1/x)² = (x² + 1/x²) + 2 ---> (x + 1/x)² = 4 + 2 ---> x + 1/x = √6 = 61/2 ---> I
b) (x + 1/x)³ = x³ + 1/x³ + 3.(x + 1/x) ---> (√6)³ = x³ + 1/x³ + 3.√6 ---> x³ + 1/x³ = 3.√6 ---> II
c) (x² + 1/x²)² = x4 + 1/x4 + 2 ---> 4² = x4 + 1/x4 + 2 ---> x4 + 1/x4 = 14 ---> III
d) (x + 1/x)5 = x5 + 5.(x3 + 1/x3) + 10.(x + 1/x) + 1/x5 ---> (√6)5 = x5 + 5.(3.√6) + 10.√6 --->
x5 + 1/x5 = 11.√6 ---> IV
e) Faça similar para (x + 1/x)7 e calcule x7 + 1/x7
f) (x4 + 1/x4)² = x8 + 1/x8 + 2 ---> 14² = x8 + 1/x8 + 2 ---> x8 + 1/x8 = 194 ---> III
x9 + 1/x9 = (x8 + 1/x8).(x + 1/x) - x7 - 1/x7
Elcioschin- Grande Mestre
- Mensagens : 73190
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Re: Sistemas de Equações de Ordem Superiores
por ALEXANDRE RESENDE DE SOUZ Dom 21 Out 2018, 16:41
Estou aqui tentando entender para chegar à resposta do Gabarito. Muito obrigado pela preciosa luz. Agora tenho um caminho a seguir.
ALEXANDRE RESENDE DE SOUZ- Padawan
- Mensagens : 99
Data de inscrição : 27/10/2010
Idade : 45
Localização : Rio Bonito, Rio de Janeiro, Brasil -
Re: Sistemas de Equações de Ordem Superiores
por ALEXANDRE RESENDE DE SOUZ Dom 21 Out 2018, 18:08
Perfeito!!! Seguindo o teu caminho encontrei a resposta. É muito trabalho braçal para pouco tempo de concurso. Esta questão, devido as expansões dos polinômios levam tempo. Obrigado pela ajuda!
ALEXANDRE RESENDE DE SOUZ- Padawan
- Mensagens : 99
Data de inscrição : 27/10/2010
Idade : 45
Localização : Rio Bonito, Rio de Janeiro, Brasil -
Re: Sistemas de Equações de Ordem Superiores
por Elcioschin Dom 21 Out 2018, 19:00
Eis então um caminho mais rápido
x² + 1/x² = 4
a) (x + 1/x)² = (x² + 1/x²) + 2 ---> (x + 1/x)² = 4 + 2 ---> x + 1/x = √6 ---> I --->Elevando I ao cubo:
b) (x + 1/x)³ = x³ + 1/x³ + 3.(x + 1/x) ---> (√6)³ = x³ + 1/x³ + 3.√6 ---> x³ + 1/x³ = 3.√6 ---> II
c) Elevando II ao cubo:
(x³ + 1/x³)³ = (3.√6)³ ---> x9 + 3.(x³)².(1/x³) + 3.x³.(1/x³)² + 1/x9 = 162.√6 --->
x9 + 1/x9 + 3.(x³ + 1/x³) = 162.√6 ---> x9 + 1/x9 + 3.(3.√6) = 162.√6 ---> x9 + 1/x9 = 153.√6
x² + 1/x² = 4
a) (x + 1/x)² = (x² + 1/x²) + 2 ---> (x + 1/x)² = 4 + 2 ---> x + 1/x = √6 ---> I --->Elevando I ao cubo:
b) (x + 1/x)³ = x³ + 1/x³ + 3.(x + 1/x) ---> (√6)³ = x³ + 1/x³ + 3.√6 ---> x³ + 1/x³ = 3.√6 ---> II
c) Elevando II ao cubo:
(x³ + 1/x³)³ = (3.√6)³ ---> x9 + 3.(x³)².(1/x³) + 3.x³.(1/x³)² + 1/x9 = 162.√6 --->
x9 + 1/x9 + 3.(x³ + 1/x³) = 162.√6 ---> x9 + 1/x9 + 3.(3.√6) = 162.√6 ---> x9 + 1/x9 = 153.√6
Elcioschin- Grande Mestre
- Mensagens : 73190
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Tópicos semelhantes» Sistemas de equações
» Equaçoes diferenciais de 2 ordem
» Cálculo IV - Equações diferenciais 1ª Ordem
» Equações Diferenciais de primeira ordem
» Sistemas de Equações
» Equaçoes diferenciais de 2 ordem
» Cálculo IV - Equações diferenciais 1ª Ordem
» Equações Diferenciais de primeira ordem
» Sistemas de Equações
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
