Desvio de partícula no campo magnético
+2
DIogoMarassi
Fernandin da Silva
6 participantes
Página 1 de 2
Página 1 de 2 • 1, 2 
 Desvio de partícula no campo magnético
Desvio de partícula no campo magnético
Uma bolinha de massa m = 2 g, eletrizada com carga q = 8μC, move-se em linha reta em um plano horizontal, com velocidade constante de 0,02 m/s.
Ao passar pelo ponto A, a bolinha penetra numa região onde existe um campo magnético uniforme e vertical, de intensidade 5T (extremamente maior que o campo magnético terrestre), que se estende até a parede vertical. Desprezando o atrito e as influências do ar, a que distância do ponto B a bolinha colidirá com a parede vertical?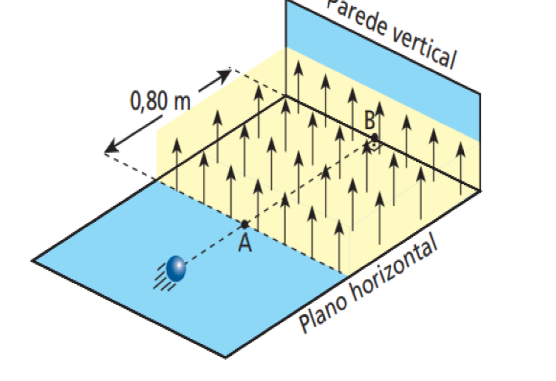
R: 0,40 m
Ao passar pelo ponto A, a bolinha penetra numa região onde existe um campo magnético uniforme e vertical, de intensidade 5T (extremamente maior que o campo magnético terrestre), que se estende até a parede vertical. Desprezando o atrito e as influências do ar, a que distância do ponto B a bolinha colidirá com a parede vertical?

R: 0,40 m
Última edição por Fernandin da Silva em Qui 04 Out 2018, 17:06, editado 1 vez(es)
Fernandin da Silva- Iniciante
- Mensagens : 12
Data de inscrição : 14/05/2018
Idade : 24
Localização : Recife-PE, Brasil
 Re: Desvio de partícula no campo magnético
Re: Desvio de partícula no campo magnético
F = B.q.V --> Calcule F
F = m.a ---> calcule a
Pela Regra dos 3 dedos da mão esquerda, a força tem sentido perpendicular à reta AB, para a direita.
A velocidade no sentido AB não muda ---> 0,8 = V.t ---> Calcule t
d = (1/2).a.t² ----> Calcule d
F = m.a ---> calcule a
Pela Regra dos 3 dedos da mão esquerda, a força tem sentido perpendicular à reta AB, para a direita.
A velocidade no sentido AB não muda ---> 0,8 = V.t ---> Calcule t
d = (1/2).a.t² ----> Calcule d

Elcioschin- Grande Mestre

- Mensagens : 73184
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Desvio de partícula no campo magnético
Re: Desvio de partícula no campo magnético
Elcio, devido a distribuição dos vetores Campo, velocidade e Força magnética a partícula não sofrerá um movimento curvilíneo Uniforme para a direita?Estou confuso nesse sentido. E essa aceleração é para qual direção, já que a velocidade no sentido de AB é constante?Elcioschin escreveu:F = B.q.V --> Calcule F
F = m.a ---> calcule a
Pela Regra dos 3 dedos da mão esquerda, a força tem sentido perpendicular à reta AB, para a direita.
A velocidade no sentido AB não muda ---> 0,8 = V.t ---> Calcule t
d = (1/2).a.t² ----> Calcule d

DIogoMarassi- Iniciante
- Mensagens : 41
Data de inscrição : 20/05/2019
Idade : 22
Localização : Rio de Janeiro, Rio de Janeiro, Brasil
 Re: Desvio de partícula no campo magnético
Re: Desvio de partícula no campo magnético
Seja r a reta onde está escrito "plano horizontal" e C o ponto onde r encontra a parede vertical
A partir do ponto A, existirão dois movimentos para a partícula carregada:
1) Um movimento retilíneo uniforme (MRU) no sentido de A para B, com velocidade
V = 0,02 m/s
AB = V.t ---> t é o tempo para a partícula chegar ao plano vertical em MRU
2) Aparece na partícula uma força F, perpendicular à reta r, isto é, uma força paralela à reta BC e com sentido de B para C (Regra dos três dedos da mão esquerda: F = B.q.V)
Devido à Lei de Newton, a toda força corresponde uma aceleração: F = m.a
Logo ---> m.a = B.q.V ---> a = B.q.V/m
Isto significa que, no sentido perpendicular a AB (paralelo a BC, de B para C) temos um MRUV (movimento retilíneo uniformemente acelerado)
A distância percorrida em MRUV vale d = (1/2).a.t²
Então, não precisa se preocupar com a forma da trajetória.
A partir do ponto A, existirão dois movimentos para a partícula carregada:
1) Um movimento retilíneo uniforme (MRU) no sentido de A para B, com velocidade
V = 0,02 m/s
AB = V.t ---> t é o tempo para a partícula chegar ao plano vertical em MRU
2) Aparece na partícula uma força F, perpendicular à reta r, isto é, uma força paralela à reta BC e com sentido de B para C (Regra dos três dedos da mão esquerda: F = B.q.V)
Devido à Lei de Newton, a toda força corresponde uma aceleração: F = m.a
Logo ---> m.a = B.q.V ---> a = B.q.V/m
Isto significa que, no sentido perpendicular a AB (paralelo a BC, de B para C) temos um MRUV (movimento retilíneo uniformemente acelerado)
A distância percorrida em MRUV vale d = (1/2).a.t²
Então, não precisa se preocupar com a forma da trajetória.

Elcioschin- Grande Mestre

- Mensagens : 73184
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Henrique R. não gosta desta mensagem
 Re: Desvio de partícula no campo magnético
Re: Desvio de partícula no campo magnético
Entendi, Elcio. Então a partícula percorre a reta AB por causa de velocidade, e percorre uma reta perpendicular a AB devido a força do campo magnético, certo? Mas se o exercício perguntasse o tipo de movimento da partícula, eu diria que é helicoidal? Devido à velocidade que faz o movimento de A para B, e à força que faz o MCUV no sentido de C. Está correto esse pensamento?Elcioschin escreveu:Seja r a reta onde está escrito "plano horizontal" e C o ponto onde r encontra a parede vertical
A partir do ponto A, existirão dois movimentos para a partícula carregada:
1) Um movimento retilíneo uniforme (MRU) no sentido de A para B, com velocidade
V = 0,02 m/s
AB = V.t ---> t é o tempo para a partícula chegar ao plano vertical em MRU
2) Aparece na partícula uma força F, perpendicular à reta r, isto é, uma força paralela à reta BC e com sentido de B para C (Regra dos três dedos da mão esquerda: F = B.q.V)
Devido à Lei de Newton, a toda força corresponde uma aceleração: F = m.a
Logo ---> m.a = B.q.V ---> a = B.q.V/m
Isto significa que, no sentido perpendicular a AB (paralelo a BC, de B para C) temos um MRUV (movimento retilíneo uniformemente acelerado)
A distância percorrida em MRUV vale d = (1/2).a.t²
Então, não precisa se preocupar com a forma da trajetória.

DIogoMarassi- Iniciante
- Mensagens : 41
Data de inscrição : 20/05/2019
Idade : 22
Localização : Rio de Janeiro, Rio de Janeiro, Brasil
 Re: Desvio de partícula no campo magnético
Re: Desvio de partícula no campo magnético
Não.
A trajetória é um arco de circunferência de raio R dado por:
Fm = Fc
B.q.V = m.V²/R
R = m.V/B.q
Esta trajetória será interrompida quando a carga atingir a parede vertical.
Nada disto, entretanto, foi solicitado no enunciado.
A trajetória é um arco de circunferência de raio R dado por:
Fm = Fc
B.q.V = m.V²/R
R = m.V/B.q
Esta trajetória será interrompida quando a carga atingir a parede vertical.
Nada disto, entretanto, foi solicitado no enunciado.

Elcioschin- Grande Mestre

- Mensagens : 73184
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Desvio de partícula no campo magnético
Re: Desvio de partícula no campo magnético
Entendi, o MCUV é interrompido. Muito obrigado, Elcio!!
Enviado pelo Topic'it
Enviado pelo Topic'it

DIogoMarassi- Iniciante
- Mensagens : 41
Data de inscrição : 20/05/2019
Idade : 22
Localização : Rio de Janeiro, Rio de Janeiro, Brasil
 Uma solução geométrica
Uma solução geométrica
Devemos antes de tudo perceber qual seria a trajetória da bolinha caso não existisse a parede vertical.
Por ela ter adentrado um Campo Magnético Uniforme, representado pelo vetor(B), com uma Velocidade vetor(v) perpendicular a este, surgirá nela uma Força Centrípeta de origem Magnética.
Podemos escrever, portanto, que:
Fm = Fctp
q*v*B*sen(90) = [(m*v^2)/R]
Isolando R, vem que:
R = (m*v)/(q*B)
Aplicando os valores fornecidos no problema, achamos que R = 1[m]
Concluímos que, se não existisse a parede vertical, a bolinha teria um Movimento Circular Uniforme de raio (R) 1[m] para a direita (Regra da Mão Espalmada).
Ocorre que, por existir a parede vertical, que se encontra a 0.8[m] de distância do ponto inicial do movimento, O MCU da partícula é interrompido antes de completar (1/4) da circunferência, que seria equivalente ao deslocamento vertical da partícula de 1[m]. Daí, podemos desenhar:
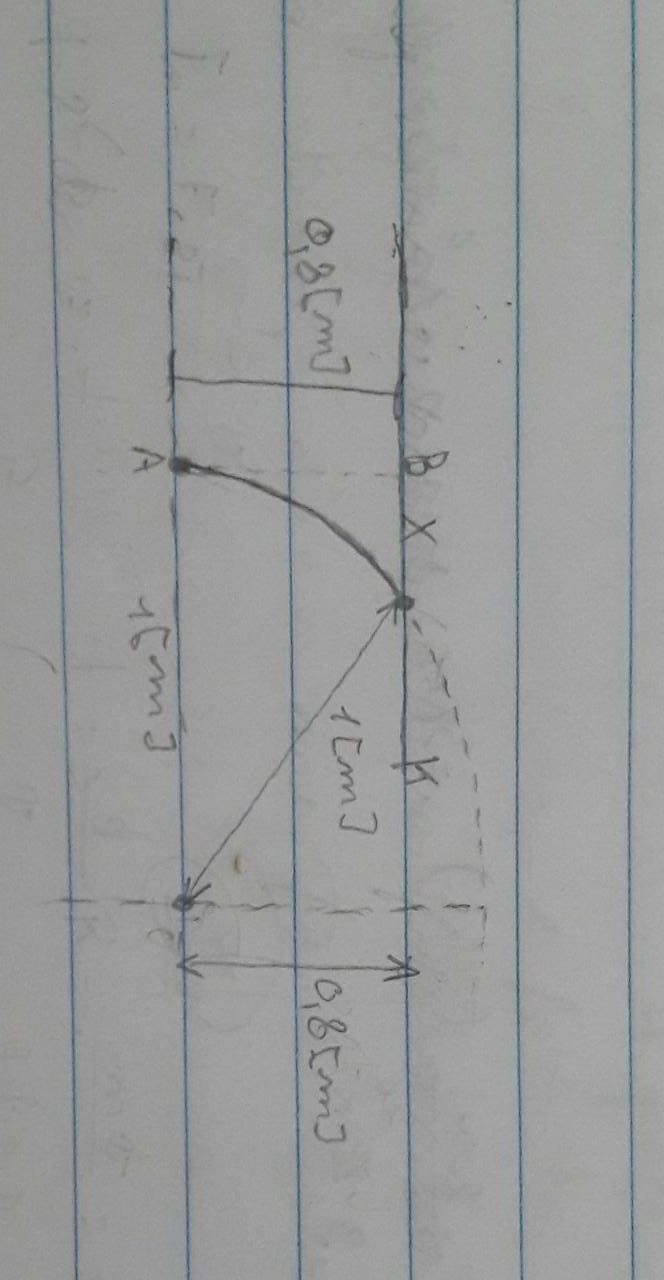
Do desenho, destaca-se o triângulo retângulo formado pelos catetos (k) e (0. e hipotenusa (1). Aplica-se Pitágoras e descobrimos que k = 0.6[m], daí achamos os deslocamento (x), que é o complemento de 0.6 para chegar em 1, ou seja, 0.4[m]
e hipotenusa (1). Aplica-se Pitágoras e descobrimos que k = 0.6[m], daí achamos os deslocamento (x), que é o complemento de 0.6 para chegar em 1, ou seja, 0.4[m]
Por ela ter adentrado um Campo Magnético Uniforme, representado pelo vetor(B), com uma Velocidade vetor(v) perpendicular a este, surgirá nela uma Força Centrípeta de origem Magnética.
Podemos escrever, portanto, que:
Fm = Fctp
q*v*B*sen(90) = [(m*v^2)/R]
Isolando R, vem que:
R = (m*v)/(q*B)
Aplicando os valores fornecidos no problema, achamos que R = 1[m]
Concluímos que, se não existisse a parede vertical, a bolinha teria um Movimento Circular Uniforme de raio (R) 1[m] para a direita (Regra da Mão Espalmada).
Ocorre que, por existir a parede vertical, que se encontra a 0.8[m] de distância do ponto inicial do movimento, O MCU da partícula é interrompido antes de completar (1/4) da circunferência, que seria equivalente ao deslocamento vertical da partícula de 1[m]. Daí, podemos desenhar:

Do desenho, destaca-se o triângulo retângulo formado pelos catetos (k) e (0.
Henrique Gouveia- Iniciante
- Mensagens : 2
Data de inscrição : 17/01/2020
Henrique R. e giordanisuelen gostam desta mensagem
 Re: Desvio de partícula no campo magnético
Re: Desvio de partícula no campo magnético
Henrique, por que você considerou o começo da trajetória curvilínea mesmo antes dos 0,8m, já que ainda não existia campo mag? Ai ele não teria sido arremessado na reta AB perpendicular a parede... não entendi isso, poderia ne explicar?Henrique Gouveia escreveu:Devemos antes de tudo perceber qual seria a trajetória da bolinha caso não existisse a parede vertical.
Por ela ter adentrado um Campo Magnético Uniforme, representado pelo vetor(B), com uma Velocidade vetor(v) perpendicular a este, surgirá nela uma Força Centrípeta de origem Magnética.
Podemos escrever, portanto, que:
Fm = Fctp
q*v*B*sen(90) = [(m*v^2)/R]
Isolando R, vem que:
R = (m*v)/(q*B)
Aplicando os valores fornecidos no problema, achamos que R = 1[m]
Concluímos que, se não existisse a parede vertical, a bolinha teria um Movimento Circular Uniforme de raio (R) 1[m] para a direita (Regra da Mão Espalmada).
Ocorre que, por existir a parede vertical, que se encontra a 0.8[m] de distância do ponto inicial do movimento, O MCU da partícula é interrompido antes de completar (1/4) da circunferência, que seria equivalente ao deslocamento vertical da partícula de 1[m]. Daí, podemos desenhar:
Do desenho, destaca-se o triângulo retângulo formado pelos catetos (k) e (0.e hipotenusa (1). Aplica-se Pitágoras e descobrimos que k = 0.6[m], daí achamos os deslocamento (x), que é o complemento de 0.6 para chegar em 1, ou seja, 0.4[m]
Última edição por Nicolly0 em Seg 18 Out 2021, 22:00, editado 1 vez(es)
Nicolly0- Iniciante
- Mensagens : 6
Data de inscrição : 12/08/2020
 Re: Desvio de partícula no campo magnético
Re: Desvio de partícula no campo magnético
Mestre Elcio, não entendi porque podemos fazer isso já que o vetor da força fica variando de direção e sentido. Tentei relacionar mais ou menos com um lançamento horizontal, mas no lançamento horizontal o vetor da força peso é constante. Poderia me explicar? Desculpe ressuscitar o tópico.Elcioschin escreveu:F = B.q.V --> Calcule F
F = m.a ---> calcule a
Pela Regra dos 3 dedos da mão esquerda, a força tem sentido perpendicular à reta AB, para a direita.
A velocidade no sentido AB não muda ---> 0,8 = V.t ---> Calcule t
d = (1/2).a.t² ----> Calcule d
Nicolly0- Iniciante
- Mensagens : 6
Data de inscrição : 12/08/2020
Página 1 de 2 • 1, 2 
 Tópicos semelhantes
Tópicos semelhantes» Campo elétrico e campo magnético desvio
» Desvio campo magnético
» Campo Magnético e Campo Elétrico Sobre Partícula
» Movimento da partícula no campo magnético
» Partícula eletrizada em campo magnético
» Desvio campo magnético
» Campo Magnético e Campo Elétrico Sobre Partícula
» Movimento da partícula no campo magnético
» Partícula eletrizada em campo magnético
Página 1 de 2
Permissões neste sub-fórum
Não podes responder a tópicos












