Teoria de geometria analitica
2 participantes
Página 1 de 1
Teoria de geometria analitica
por mariaheloisac Ter 18 Set 2018, 12:33
Mack. Os pontos P(x,y) do plano, tais que cos(x+y) = 0, constituem:
a - uma reta que passa pelo ponto P (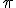
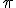/2, /2)
b - uma cossenóide
c - uma hiperbole
d - um feixe de retas paralelas a bissetriz dos quadrantes pares
e - um feixe de retas concorrentes em x = 0 e y = 0
a resposta é a letra d, mas eu nao estou entendo o porque da resposta e o que tem de errado nas outras alternativas
a - uma reta que passa pelo ponto P (
b - uma cossenóide
c - uma hiperbole
d - um feixe de retas paralelas a bissetriz dos quadrantes pares
e - um feixe de retas concorrentes em x = 0 e y = 0
a resposta é a letra d, mas eu nao estou entendo o porque da resposta e o que tem de errado nas outras alternativas
mariaheloisac- Iniciante
- Mensagens : 8
Data de inscrição : 24/09/2017
Idade : 24
Localização : Curitiba, Parana, Brasil
Re: Teoria de geometria analitica
por Elcioschin Ter 18 Set 2018, 12:57
cos(x + y) = 0
Temos duas possibilidades, na 1ª volta: x + y = pi/2 e x + y = 3.pi/2
Solução geral ---> x + y = pi/2 + k.pi ---> com k inteiro --->
y = - x + (pi/2 + k.pi)
Retas paralelas aos quadrantes pares (- x). Para cada valor de k existe uma reta.
Temos duas possibilidades, na 1ª volta: x + y = pi/2 e x + y = 3.pi/2
Solução geral ---> x + y = pi/2 + k.pi ---> com k inteiro --->
y = - x + (pi/2 + k.pi)
Retas paralelas aos quadrantes pares (- x). Para cada valor de k existe uma reta.
Elcioschin- Grande Mestre
- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Romanelo gosta desta mensagem
mariaheloisac- Iniciante
- Mensagens : 8
Data de inscrição : 24/09/2017
Idade : 24
Localização : Curitiba, Parana, Brasil
Tópicos semelhantes» CIRCUNFERÊNCIA
» Geometria Plana-Teoria.
» Geometria + Teoria dos números (OCM 2019)
» Sobre a teoria de geometria de posição
» Geometria Analítica - Teoria angular
» Geometria Plana-Teoria.
» Geometria + Teoria dos números (OCM 2019)
» Sobre a teoria de geometria de posição
» Geometria Analítica - Teoria angular
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
