Força Elástica e a Lei de Hooke (Sistemas Massa-Mola)

Publicado originalmente pelo Euclides numa página extra.



Elasticidade dos materiais, tração e tensão, o módulo de Young, o coeficiente de restituição, a lei de Hooke e oscilações em MHS.

- Trabalhando com molas


As figuras acima mostram uma mesma mola à qual está ligado um bloco de massa M. O sistema então é distendido de um alongamento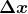 , ou contraído na mesma extensão. Em ambos os casos a mesma energia potencial é acumulada na mola.

Se a força for retirada e o sistema abandonado, sem que haja atritos ou resistências dissipativas, então o sistema massa-mola entrará em uma oscilação de amplitude delta x em torno do ponto de equilíbrio no qual a força resultante no sistema é nula, assim como a energia potencial elástica e a energia mecânica é devida exclusivamente à energia cinética do bloco.

Pelo princípio da conservação da energia, a energia mecânica do sistema oscilante em um MHS será dada pela soma dos seus conteúdos cinético e potencial (por simplicidade trataremos o termo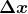 simplesmente como x)


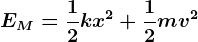
Como acabamos de ver, a energia potencial no ponto de equilíbrio (x=0) é nula e, portanto, a velocidade é máxima. Analogamente nos pontos de distensão (+x), ou contração (-x), máximas a energia potencial é máxima e a velocidade será nula, o que é intuitivamente coerente pois são os pontos de inversão de sentido do movimento.

Esse movimento oscilatório (MHS) terá um período, ou seja, o menor tempo em que uma mesma posição é assumida consecutivamente, dado por

-- Molas seccionadas e associações de molas

O que poderemos esperar da constante elástica de uma mola se a seccionarmos em duas, três ou mais partes? As novas molas assim produzidas terão as mesma características da mola inicial, exceto seu comprimento. Como isso afeta a constante elástica?

Foi por esta razão que na nossa abordagem inicial mencionamos o módulo de Young. Este, assim como a densidade ou a dureza é uma propriedade física de cada material e assim uma mesma constante para a mola original e suas partes cortadas. Lembremo-nos da equação (1)



olhando-se essa expressão fica fácil ver que se cortarmos uma mola cujo coeficiente seja k em n partes de comprimentos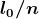 , o coeficiente de elasticidade de cada parte será nk.

Isso já pode nos sugerir outro conceito. Se agora associarmos essas n molas assim obtidas em série deveremos obter novamente a mola original e sua constante elástica.

A constante elástica de uma associação de molas em série é menor que a menor das constantes de cada mola associada. De fato, teremos a constante da mola equivalente expressa por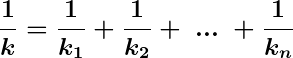

Para uma associação de molas em série

Quando associadas em paralelo teremos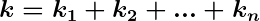

Exemplo 1


Larga-se a bola na posição indicada na figura ao lado. O comprimento do fio é 2lo. Qual é o alongamento máximo da mola?

A energia potencial de altura da bola deve ser toda convertida em potencial elástica da mola.



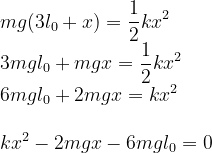
devemos procurar a solução positiva dessa equação do segundo grau



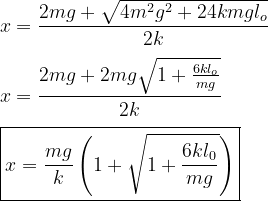
Exemplo 2

Um sistema oscilante massa-mola possui energia mecânica igual a 2,0 J e amplitude de 0,10m e velocidade máxima 1,2m/s. Determine:

I) A constante elástica da mola
II) A massa
III) A frequência das oscilações



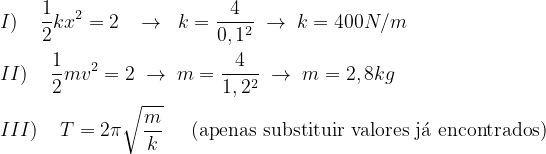
O MHS de um ponto de vista circular e uniforme

Pelo que já vimos, o MHS, em si, não é um movimento uniforme. A força responsável pelo movimento é variável (em função da distensão da mola ou posição da massa), acarretando uma variação da velocidade de maneira regular, mas não constante, ou seja, uma aceleração variável.

Entretanto, o Movimento Harmônico Simples pode ser entendido como sendo a projeção de um MCU sobre um diâmetro da circunferência.


O MCU, representado pelo ponto vermelho, tem suas posições consecutivas e velocidade projetadas sobre um diâmetro. Essa projeção realiza um MHS com posição de equilíbrio no centro da circunferência.

A figura a seguir mostra a projeção de um MCU sobre o diâmetro horizontal da trajetória circular.

Daremos ao tamanho do raio o nome de amplitude do MHS e a designaremos por A. Vemos então que a posição x pode ser expressa como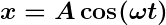

como já sabemos calcular o período de um MHS em um sistema massa-mola, não teremos dificuldade para encontrar a velocidade angular (às vezes chamada de frequência angular)



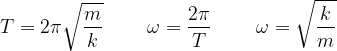
Por derivação poderemos obter as expressões para a velocidade e a aceleração do MHS em qualquer instante



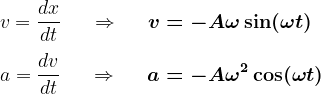
os sinais (sentidos) da velocidade e aceleração são dados pelas funções circulares significando o sentido em relação ao eixo orientado da esquerda para a direita, com origem no centro da circunferência. As funções circulares igualmente permitem identificar os valores máximos alcançados pela velocidade e aceleração, respecticvamente quando seno e cosseno assumem seus valores máximos



esses valores ocorrem, para a velocidade, quando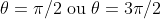 , coincidindo com as passagens pela origem, posição de equilíbrio, o que reafirma o fato de a energia cinética ser máxima nessa posição. A aceleração é nula nessas posições em que a energia potencial elástica é nula.

A velocidade é nula para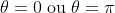 e a aceleração assume seus valores máximos, correspondendo às passagens nos pontos de elongação máxima, o que nos diz que nessas posições a energia potencial é máxima e a cinética é nula.

Exercícios resolvidos

1) Uma mola de comprimento natural 3m e cte elástica 10 N/m tem uma extremidade fixada a 10m do solo e, em sua outra extremidade, está presa a um corpo de 2Kg. No instante t0, esse corpo se encontra a uma altura de 9m do solo, com velocidade nula. Sabendo que o movimento subsequente desse corpo se dá sobre a reta vertical em que a mola se encontra e que tal corpo sofre apenas a ação das forças elásticas e gravitacional, qual é a intensidade da velocidade máxima que esse corpo atingirá em seu movimento?

A imagem abaixo ajudará a compreender:


No início a mola se encontra comprimida em 2m. A energia associada ao corpo é:



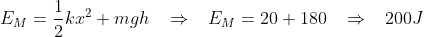
a velocidade será máxima na altura em que a força elástica (para cima) igualar o peso do corpo



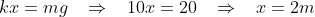
a mola estará distendida 2m para baixo e o corpo estará a uma altura de 5m (examine a figura). A energia mecânica pode ser novamente equacionada:



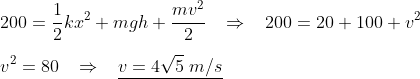
2) Determinar a mínima deformação que a mola de constante k deve experimentar, se a barra homogênea de massa m está a ponto de deslizar.


Na condição de equilíbrio as somas das forças em cada eixo devem se anular



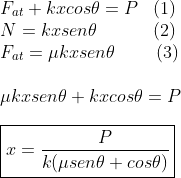
3) Devemos aplicar uma força de módulo 80 N para manter em repouso um bloco em x=-2 cm.A partir dessa posição,deslocamos o bloco lentamente de modo que a força realiza um trabalho de +4 J sobre o sistema massa-mola;a partir daí ,mantemos o bloco em repouso novamente.Qual é a posição do bloco? O bloco está sobre uma superfície horizontal.