Cone- Altura

por Liliana Rodrigues Sex 10 Ago 2018, 19:33

Para construir um funil a partir de um disco de alumínio de centro O e raio R = 16 cm, retira-se do disco um setor circular de ângulo central \Theta = 225º. Em seguida, remove-se um outro setor circular, de raio r = 1 cm. Para finalizar, soldam-se as bordas AC e BD. O processo de construção do funil está representado nas figuras abaixo.

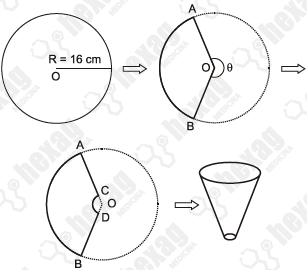
A medida da altura do funil é:
a) 2√39 cm.
b) 15√39/8 cm.
c) √(55)/8 cm.
d) 2 √55 cm.
e) 15√(55)/8 cm.

por **Elcioschin** Sex 10 Ago 2018, 20:06

Começando

A geratriz total do cone é g = R ---> g = 16
O ângulo do setor aproveitado vale 360º - 225º = 135º

Seja R' o raio da base maior do cone e do tronco de cone e seja r o raio da base menor do tronco de cone:

360º --- 2.pi.R
135º --- p .......... p = perímetro do arco de setor de 135º ---> p = 0,75.pi.R ---> p = 12.pi

12.pi = 2.pi.R' ---> R' = 6 cm

De modo similar, calcule r e depois, por semelhança de triângulos, calcule h

por Unßer Sex 10 Ago 2018, 20:41

Vou subdividir a questão em etapas.
Primeiro precisamos achar os raios das bases menor e maior do funil.

A) Se na Base MAIOR.

360 > 2πR | Se R=16cm |
(360-225) > 2πR' |Comprimento setorial vira um circulo como visto|
R'= 6 cm

Se na Base MENOR.

360 > 2πr | Se r=1cm |
(360-225) > 2πr' |Comprimento setorial vira um circulo como visto|
R'= 3/8 cm

B) Essa fase é a mais lógica

Se o meu raio inicial coincidiria com a geratriz(fique calma irei mostrar uma imagem) do tronco de cone.No caso, eu tinha 16 cm de, só que eu tirei 1 cm(Base menor) , restando 15 cm de geratriz.

Sei que talvez seja difícil imaginar, veja está imagem:

o g= é igual a geratriz , veja essas imagens:

Cone- Altura Questao_024445_15764_1409470_

Está te ajudando? se estiver , perfeito.

Agora iremos para a última etapa.

C) Teorema de Pitágoras

Imagina a primeira imagem postada, veja que o raio da maior era 8 cm só que retiramos 5 cm , restando 3 cm.

Se fizermos o mesmo exemplo, vamos perceber 6cm - 3/8cm = 45/8cm

Aplicando Pitágoras, sendo a geratriz a hipotenusa, H(altura) um dos catetos, assim como 45/8cm.

15²=(45/

² + H²

Sabemos que 45=15.3

15²=9.15²/8² + H²

H²=55.15²/8²

H= 15√(55)/8 cm

Obviamente, a questão pode ser feita mais rapidamente, porém não seu seu nível de dificuldade na questão, meu objetivo é tornar seu entendimento mais fácil, e facilitar sua compreensão. Espero ter ajudado.