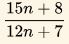Provar a sentença
5 participantes
Página 1 de 1

brasileiro312- Jedi

- Mensagens : 304
Data de inscrição : 28/02/2017
Idade : 22
Localização : Rio de Janeiro, Rio de Janeiro, Brasil
 Re: Provar a sentença
Re: Provar a sentença
Não existe k pertencente aos naturais que represente a fração, logo, é irredutível
justanightmare- Jedi

- Mensagens : 280
Data de inscrição : 25/08/2017
Idade : 24
Localização : Belo Horizonte, Minas Gerais, Brasil
 Re: Provar a sentença
Re: Provar a sentença
Pesquise sobre o algoritmo de Euclides e conclua que (15n +8, 12n + 7) = 1
Night, acredito que não possamos realizar tal procedimento, pois não há garantia que a fração seja inteira.
Veja que 8/16 é redutível, mas não pertence aos inteiros.
Night, acredito que não possamos realizar tal procedimento, pois não há garantia que a fração seja inteira.
Veja que 8/16 é redutível, mas não pertence aos inteiros.

mts_007- Iniciante
- Mensagens : 7
Data de inscrição : 09/07/2018
Idade : 27
Localização : Crato/CE
 Re: Provar a sentença
Re: Provar a sentença
Você tem razão mts, esses dias eu estava fazendo uma questão semelhante em que n teria que ser natural, entre outras coisas, e o método que eu tinha utilizado era esse.
Valeu por avisar.
Valeu por avisar.
justanightmare- Jedi

- Mensagens : 280
Data de inscrição : 25/08/2017
Idade : 24
Localização : Belo Horizonte, Minas Gerais, Brasil
 Re: Provar a sentença
Re: Provar a sentença
Vamos chamar o mdc entre eles de d, temos que:
d|15n+8 (I)
d|12n+7
d|(12n+7).5 -4.(15n+
d|3
d = 1 ou d = 3
d não pode ser 3 pois de (I), por exemplo, deveríamos ter que d|8 o que implicaria que 3|8, o que não é verdade, então devemos ter d = 1 e portanto a fração é irredutível.
d|15n+8 (I)
d|12n+7
d|(12n+7).5 -4.(15n+
d|3
d = 1 ou d = 3
d não pode ser 3 pois de (I), por exemplo, deveríamos ter que d|8 o que implicaria que 3|8, o que não é verdade, então devemos ter d = 1 e portanto a fração é irredutível.
fantecele- Fera

- Mensagens : 1225
Data de inscrição : 14/09/2014
Idade : 27
Localização : Nova Venécia-ES, Brasil
 Re: Provar a sentença
Re: Provar a sentença
Poderia me explicar melhor como faço pelo algoritmo de Euclides, por favor?mts_007 escreveu:Pesquise sobre o algoritmo de Euclides e conclua que (15n +8, 12n + 7) = 1
Night, acredito que não possamos realizar tal procedimento, pois não há garantia que a fração seja inteira.
Veja que 8/16 é redutível, mas não pertence aos inteiros.
Ana29Carolina- Padawan

- Mensagens : 88
Data de inscrição : 13/04/2016
Idade : 24
Localização : Carmo da Mata-MG, Brasil
 Re: Provar a sentença
Re: Provar a sentença
Ana29Carolina escreveu:
Poderia me explicar melhor como faço pelo algoritmo de Euclides, por favor?
Não tem muito segredo,
mdc(15n +8, 12n + 7) = mdc( 15n +8 - (12n + 7), 12n + 7 ) = mdc( 3n +1, 12n + 7 )
mdc( 3n +1, 12n + 7 ) = mdc( 3n +1, 12n + 7 - 4*(3n + 1) ) = mdc( 3n +1, 3 )
mdc( 3n +1, 3 ) = mdc( 3n +1 - 3*n, 3 ) = mdc( 1, 3 )
mdc( 1,3 ) = 1

mts_007- Iniciante
- Mensagens : 7
Data de inscrição : 09/07/2018
Idade : 27
Localização : Crato/CE
 Re: Provar a sentença
Re: Provar a sentença
Ah ta! Agora sim, compreendi! Muito obrigada! 
Ana29Carolina- Padawan

- Mensagens : 88
Data de inscrição : 13/04/2016
Idade : 24
Localização : Carmo da Mata-MG, Brasil
 Tópicos semelhantes
Tópicos semelhantes» Provar sentença
» Radiciação - Sentença
» A sentença de f[f(x)]
» A sentença 3 ⊂ {3, {3}}
» Sentença X e Y... !!
» Radiciação - Sentença
» A sentença de f[f(x)]
» A sentença 3 ⊂ {3, {3}}
» Sentença X e Y... !!
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos