circuferência e retas

por DanielXD12 Dom 08 Jul 2018, 11:58

São dados, no plano cartesiano de origem O, a circuferência de equação x²+y²=13, o ponto A(1,-6) e a reta s, que passa por A e é paralela r: x+y+3=-. Seja B o ponto de maior abscissa em que a reta s intercepta a circuferência. Assim sendo, determine a reta t, tangente a circuferência no ponto B.
a) 2x+3y+13=0
b) 3x-2y=0
c) 2x+3y-13=0
d) 3x-2y-15=0
e) 2x+3y+16=0

Fui tentar fazer e realmente não consegui, creio que ela possa não ter solução se meu raciocínio tiver correto. Mas, aguardo a resposta de alguém ^^

por **Giovana Martins** Dom 08 Jul 2018, 13:09

O enunciado têm problemas. Qual a reta r?

Mesmo com problemas no enunciado, creio que ainda dê para resolver a questão.

O coeficiente angular da reta r, e também da reta s, visto que r // s, teoricamente é igual a -1.

Como A(1,-6) ∈ s: x+y=-5 (equação da reta s)

Do sistema formado por x²+y²=13 e x+y=-5, obtêm-se os pontos: B(-2,-3) e C(-3,-2).

Seja m o coeficiente angular da reta u que contém o centro O(0,0) da circunferência e o ponto B(-2,-3). A partir dos pontos B(-2,-3) e O(0,0), conclui-se que o coeficiente angular da reta u é dado por m=3/2. Como a reta t é tangente à circunferência no ponto B(-2,-3), infere-se que neste ponto t 丄 u, logo, o coeficiente angular da reta t é dado por: m'=-1/m=-2/3.

Sabendo que m'=-2/3 e B(-2,-3) podemos encontrar a reta t.

y+3=(-2/3)(x+2) → 2x+3y+13=0

por **Giovana Martins** Dom 08 Jul 2018, 13:10

Em breve eu posto uma imagem.

por **Giovana Martins** Dom 08 Jul 2018, 13:21

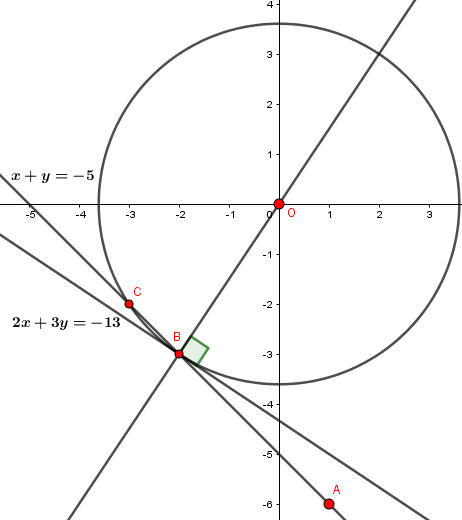
Esta questão também poderia ser resolvida utilizando o conhecimento sobre derivadas.

A derivada de x²+y²=13 no ponto B(-2,-3) nos fornece o coeficiente angular da reta t. A seguir tem-se o cálculo da derivada de x²+y²=13 no ponto B(-2,-3).

Derivando implicitamente a equação x²+y²=13:

(x²+y²)'=(13)' → 2x+2yy'=0 → y'=-x/y

No ponto B(-2,-3): y'=-[(-2)/(-3)] → y'=-2/3

y+3=y'(x+2) → y+3=(-2/3)(x+2) → 2x+3y+13=0

por DanielXD12 Dom 08 Jul 2018, 18:34

Obrigado, eu deduzi que o maior valor de x deveria ser positivo... ai errei x.x

por DanielXD12 Dom 08 Jul 2018, 18:55

Amigo, ainda não entendi como você encontrou o b e c. Eu fiz por substituição o sistema usando o y ao quadrado na equação da reta s na equação da circuferência e acabei achando um x muito feio. Você pode me explicar como você chegou a esses pontos ?

por DanielXD12 Dom 08 Jul 2018, 19:01

Consegui. Eu que errei besteira ao fazer a conta.

por **Giovana Martins** Dom 08 Jul 2018, 19:05

"Amigo, ainda não entendi como você encontrou o b e c. Eu fiz por substituição o sistema usando o y ao quadrado na equação da reta s na equação da circuferência e acabei achando um x muito feio. Você pode me explicar como você chegou a esses pontos ?"

Eu não sou um rapaz.

x²+y²=13 (I)

y=-x-5 (II)

x²+(-x-5)²=13 → 2x²+10x+12=0 → x'=-2 ou x''=-3

x'=-2 em (I): y=-3, logo, B(-2,-3).

x''=-3 em (I): y=-2, logo, C(-3,-2).

por DanielXD12 Dom 08 Jul 2018, 19:34

Certo. Obrigado. Desculpe, não olhei seu nome. Disse amigo, porque era de costume. Em relação aos pontos, fiz e consegui sim. Mas não entendi como você conseguio sair tão rápido do coeficiente angular da reta tangente e foi para a equação da reta, pois da maneira que fiz levei bastante tempo. Você poderia me explicar por favor ?

por **Giovana Martins** Dom 08 Jul 2018, 19:43

"Certo. Obrigado. Desculpe, não olhei seu nome. Disse amigo, porque era de costume."

Sem problemas.

Eu omiti alguns cálculos na resolução, pois certamente você deve saber fazê-los.

Por exemplo, nesta parte: y+3=(-2/3)(x+2) → 2x+3y+13=0. Aqui eu apenas apresentei o resultado final, o mesmo vale para o cálculo do coeficiente angular, eu só apresentei o resultado final.