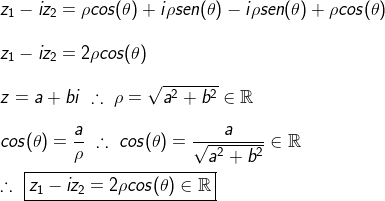Forma Trigonométrica de Um Número Complexo
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Forma Trigonométrica de Um Número Complexo
Forma Trigonométrica de Um Número Complexo
Olá, tudo bem? Espero que sim! Poderiam me ajudar com esse exercício? Agradeço desde já!
Dados os números complexos:
Z1=ρ.( cosθ + i.senθ)
Z2=ρ.( senθ + i.cosθ)
Assinale a alternativa correta:
a) Z1 e Z2 são conjugados
b) Z1 + Z2 é um número real
c) Z1.Z2 é um número real
d) Z1 - i.Z2 é um número real
e) Z1 - Z2 é um número real
Resposta: E
Dados os números complexos:
Z1=ρ.( cosθ + i.senθ)
Z2=ρ.( senθ + i.cosθ)
Assinale a alternativa correta:
a) Z1 e Z2 são conjugados
b) Z1 + Z2 é um número real
c) Z1.Z2 é um número real
d) Z1 - i.Z2 é um número real
e) Z1 - Z2 é um número real
Resposta: E
cami_cam- Padawan

- Mensagens : 67
Data de inscrição : 15/06/2018
Idade : 31
Localização : São Paulo, SP, BR
 Re: Forma Trigonométrica de Um Número Complexo
Re: Forma Trigonométrica de Um Número Complexo
Olá princesa , tudo bem sim e com vc ?
Então , z1 está na forma polar normal , pois se representarmos ele no plano de argand-gauss cos(theta) está no eixo y , Sen(theta) está no eixo y , e sua coordenada quando ligados a origem nos dará o módulo do número complexo ( rho).
Z1 pode ser chamado de (rho)cis(theta).
Agora vamos fazer algumas relações algébricas para chegar em um valor bonitinho para z2.
Repare que -i^2=1
Então temos :
Z2=(rho)(-i^2)[Sen(theta)+cós(theta)i]
Colocando apenas (-i) para dentro dos colchetes , temos:
Z2=(i)(rho)[cós(theta)-isen(theta)]
Agora relembramos que a função cosseno é uma função par e a função seno é ímpar , logo podemos escrever da seguinte maneira:
Z2=i(rho)[cós(-theta)+isen(-theta)]
Z2=i(rho)[cis(-theta)]
Agora faremos operação por operação para as alternativas.
a) repare que Z2 seria conjugado de Z1 apenas se Z2=(rho)[cis(-theta)] , o que não é verdade , como demonstrado .
b)caso olharmos para os valores dados pelo enunciado , veremos que não é verdade.
Pois Z1+Z2=(rho)[Sen(theta)+cós(theta)]+i[Sen(theta)+cós(theta)].
A Im(Z1+Z2) não é igual a 0 para ser um número real.
c)z1.z2=(rho)^2(i)cis(theta).cis(-theta)
Z1.z2=(rho)^2(i)cis(0)
Z1.z2=(rho)^2(i) , logo é um número imaginário .
d)Z1-(i)Z2= (rho)cis(theta)-(i)^2(rho)cis(-theta)
Z1-(i)Z2=(rho)cis(theta)+(rho)cis(-theta)
Z1-(i)Z2=(rho)[2 cós(theta)].
e)Z1-Z2=(rho)[cos(theta)-sen(theta)]+i[Sen(theta)-cos(theta)].
Bom acho eu que seja d).
Então , z1 está na forma polar normal , pois se representarmos ele no plano de argand-gauss cos(theta) está no eixo y , Sen(theta) está no eixo y , e sua coordenada quando ligados a origem nos dará o módulo do número complexo ( rho).
Z1 pode ser chamado de (rho)cis(theta).
Agora vamos fazer algumas relações algébricas para chegar em um valor bonitinho para z2.
Repare que -i^2=1
Então temos :
Z2=(rho)(-i^2)[Sen(theta)+cós(theta)i]
Colocando apenas (-i) para dentro dos colchetes , temos:
Z2=(i)(rho)[cós(theta)-isen(theta)]
Agora relembramos que a função cosseno é uma função par e a função seno é ímpar , logo podemos escrever da seguinte maneira:
Z2=i(rho)[cós(-theta)+isen(-theta)]
Z2=i(rho)[cis(-theta)]
Agora faremos operação por operação para as alternativas.
a) repare que Z2 seria conjugado de Z1 apenas se Z2=(rho)[cis(-theta)] , o que não é verdade , como demonstrado .
b)caso olharmos para os valores dados pelo enunciado , veremos que não é verdade.
Pois Z1+Z2=(rho)[Sen(theta)+cós(theta)]+i[Sen(theta)+cós(theta)].
A Im(Z1+Z2) não é igual a 0 para ser um número real.
c)z1.z2=(rho)^2(i)cis(theta).cis(-theta)
Z1.z2=(rho)^2(i)cis(0)
Z1.z2=(rho)^2(i) , logo é um número imaginário .
d)Z1-(i)Z2= (rho)cis(theta)-(i)^2(rho)cis(-theta)
Z1-(i)Z2=(rho)cis(theta)+(rho)cis(-theta)
Z1-(i)Z2=(rho)[2 cós(theta)].
e)Z1-Z2=(rho)[cos(theta)-sen(theta)]+i[Sen(theta)-cos(theta)].
Bom acho eu que seja d).

Matheus Tsilva- Fera

- Mensagens : 1240
Data de inscrição : 16/07/2015
Idade : 26
Localização : Uberaba, MG
 Re: Forma Trigonométrica de Um Número Complexo
Re: Forma Trigonométrica de Um Número Complexo
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8546
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: Forma Trigonométrica de Um Número Complexo
Re: Forma Trigonométrica de Um Número Complexo
Oi, Matheus e Giovana, tudo bem também.
Muito obrigada pela resolução dos dois!
Vou tentar refazer sozinha após as orientações.
Sobre o gabarito, é questão autoral do Poliedro, então creio que seja passível de erro mesmo, já que os dois chegaram na mesma resposta!
Obrigada pessoal, bom final de semana!
Muito obrigada pela resolução dos dois!
Vou tentar refazer sozinha após as orientações.
Sobre o gabarito, é questão autoral do Poliedro, então creio que seja passível de erro mesmo, já que os dois chegaram na mesma resposta!
Obrigada pessoal, bom final de semana!
cami_cam- Padawan

- Mensagens : 67
Data de inscrição : 15/06/2018
Idade : 31
Localização : São Paulo, SP, BR
 Tópicos semelhantes
Tópicos semelhantes» Forma trigonométrica- número complexo
» Número complexo forma trigonométrica
» Número complexo e forma trigonométrica
» forma algébrica de um número complexo
» Número complexo, forma a+bi
» Número complexo forma trigonométrica
» Número complexo e forma trigonométrica
» forma algébrica de um número complexo
» Número complexo, forma a+bi
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos