limites
2 participantes
Página 1 de 1
limites
por Matheus de C. Goulart Dom 10 Jun 2018, 12:36
Boa tarde , me deparei hoje com o seguinte limite :
e tentei resolve-lo da seguinte forma :
1)multipliquei o denominador e o numerador por :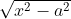
e obtive :
(\sqrt{x^2-a^2})}{x^2-a^2} "\lim x->a \frac{(\sqrt{x}-\sqrt{a}+\sqrt{x-a})(\sqrt{x^2-a^2})}{x^2-a^2}")
Fiz a distributiva e obtive :
(\sqrt{x})-(\sqrt{x^2-a^2})(\sqrt{a})+(\sqrt{x^2-a^2})(\sqrt{x-a}))}{x^2-a^2} "\lim x->a \frac{(\sqrt{x^2-a^2})(\sqrt{x})-(\sqrt{x^2-a^2})(\sqrt{a})+(\sqrt{x^2-a^2})(\sqrt{x-a}))}{x^2-a^2}")
reescrevi o terceiro termo do numerador como:
(x+a)(x-a)} "\sqrt{(x-a)(x+a)(x-a)}")
^2(x+a)} "\sqrt{(x-a)^2(x+a)}")
(\sqrt{(x+a)}) "(x-a)(\sqrt{(x+a)})")
Ficando assim:
(\sqrt{x})-(\sqrt{x^2-a^2})(\sqrt{a})+(\sqrt{x+a})(x-a)}{(x-a)(x+a)} "\lim x->a \frac{(\sqrt{x^2-a^2})(\sqrt{x})-(\sqrt{x^2-a^2})(\sqrt{a})+(\sqrt{x+a})(x-a)}{(x-a)(x+a)}")
a partir dessa parte eu travei ,cometi algum erro??? alguem pode me dar uma dica de como prosseguir a partir dessa parte?
grato pela atenção!
obs: o Wolframalpha diz que a resposta é:
e tentei resolve-lo da seguinte forma :
1)multipliquei o denominador e o numerador por :
e obtive :
Fiz a distributiva e obtive :
reescrevi o terceiro termo do numerador como:
Ficando assim:
a partir dessa parte eu travei ,cometi algum erro??? alguem pode me dar uma dica de como prosseguir a partir dessa parte?
grato pela atenção!
obs: o Wolframalpha diz que a resposta é:
Última edição por Matheus de C. Goulart em Dom 10 Jun 2018, 15:34, editado 1 vez(es)
Matheus de C. Goulart- Iniciante
- Mensagens : 2
Data de inscrição : 08/09/2017
Idade : 26
Localização : Rj , Rio de Janeiro , Brasil
Re: limites
por Willian Honorio Dom 10 Jun 2018, 15:19
Falta apenas cancelar o termo (x-a) no denominador, vide que temos uma indeterminação do tipo 0/0. Para isso, é necessário fatorar a expressão no numerador. Coloque o termo √(x²-a²) em evidência nos dois primeiros fatores do numerador. Após isso, utilize a fatoração a²-b²=(a-b)(a+b), com a=√x e b=√a. Achará: √x-√a=(x-a)/√x+√a. Aí coloque o termo x-a em evidência novamente, cancelando o termo x-a do denominador que levanta este limite. A resposta que encontrará, aplicando a definição, será √2.a/2.a que é equivalente à encontrada no Wolfram. Espero que essa dica te ajude, caso contrário, só falar que farei o cálculo detalhado.
Willian Honorio- Matador
- Mensagens : 1271
Data de inscrição : 27/04/2016
Idade : 27
Localização : São Paulo
Re: limites
por Matheus de C. Goulart Dom 10 Jun 2018, 15:30
Muito obrigado ! , eu também tentei resolver e encontrei exatamente a mesma resposta que a sua , porém não sabia que eram equivalentes .
novamente obrigado pela atenção!
edit: agora que percebi que essa resposta é apenas a resposta do Wolfram não racionalizada
.
novamente obrigado pela atenção!
edit: agora que percebi que essa resposta é apenas a resposta do Wolfram não racionalizada
.
Matheus de C. Goulart- Iniciante
- Mensagens : 2
Data de inscrição : 08/09/2017
Idade : 26
Localização : Rj , Rio de Janeiro , Brasil
Re: limites
por Willian Honorio Dom 10 Jun 2018, 15:42
kkkkkk, faz parte. Essa é a resposta do Wolfram racionalizada . Acredito que a programação deles não se importe em racionalizar resultados finais por meras questões práticas, ou até mesmo o levantamento de limites no programa pode ter sido feito de maneira diferente, que conduz àquele resultado. Em suma, a resposta final é a mesma e não há o que se preocupar.
Willian Honorio- Matador
- Mensagens : 1271
Data de inscrição : 27/04/2016
Idade : 27
Localização : São Paulo
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
