Interpretação da derivada de um gráfico
2 participantes
Página 1 de 1
Interpretação da derivada de um gráfico
por martinimarcos Qua 09 maio 2018, 21:14
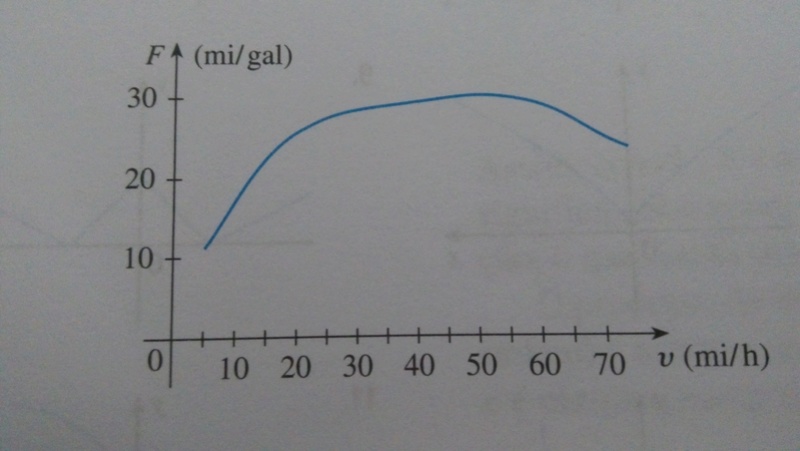
O gráfico (do Departamento de Energia dos EUA) mostra como a velocidade do carro afeta o rendimento do combustível. O rendimento do combustível F é medido em milhas por galão e a velocidade v é medida em milhas por hora.
a) qual o significado da derivada de f?
b) em qual velocidade você deve dirigir se quer economizar combustível?
a) qual o significado da derivada de f?
b) em qual velocidade você deve dirigir se quer economizar combustível?
martinimarcos- Iniciante
- Mensagens : 22
Data de inscrição : 23/03/2018
Idade : 24
Localização : Florianópolis
Re: Interpretação da derivada de um gráfico
por Elcioschin Qua 09 maio 2018, 22:19
A derivada de F, em cada ponto do gráfico, é numericamente igual ao valor da tangente trigonométrica do ângulo θ formado pelo eixo v e pela reta tangente ao gráfico, no ponto dado (é o coeficiente angular da reta tangente)
A unidade da derivada seria (mi/gal)(mi/h) = 1/(gal/h) = consumo por unidade de tempo
O que se deseja é o menor consumo de combustível. Isto acontece quando tgθ = 0, isto é quando a reta tangente é paralela ao eixo v. Isto acontece aproximadamente para v = 50 mi/h ~= 80 km/h
A unidade da derivada seria (mi/gal)(mi/h) = 1/(gal/h) = consumo por unidade de tempo
O que se deseja é o menor consumo de combustível. Isto acontece quando tgθ = 0, isto é quando a reta tangente é paralela ao eixo v. Isto acontece aproximadamente para v = 50 mi/h ~= 80 km/h
Elcioschin- Grande Mestre
- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Re: Interpretação da derivada de um gráfico
por martinimarcos Dom 13 maio 2018, 11:04
ObrigadoElcioschin escreveu:A derivada de F, em cada ponto do gráfico, é numericamente igual ao valor da tangente trigonométrica do ângulo θ formado pelo eixo v e pela reta tangente ao gráfico, no ponto dado (é o coeficiente angular da reta tangente)
A unidade da derivada seria (mi/gal)(mi/h) = 1/(gal/h) = consumo por unidade de tempo
O que se deseja é o menor consumo de combustível. Isto acontece quando tgθ = 0, isto é quando a reta tangente é paralela ao eixo v. Isto acontece aproximadamente para v = 50 mi/h ~= 80 km/h
martinimarcos- Iniciante
- Mensagens : 22
Data de inscrição : 23/03/2018
Idade : 24
Localização : Florianópolis
Tópicos semelhantes» Interpretação do gráfico
» Interpretação de gráfico
» Interpretação de gráfico
» Interpretação de gráfico
» Interpretação da notação da função derivada
» Interpretação de gráfico
» Interpretação de gráfico
» Interpretação de gráfico
» Interpretação da notação da função derivada
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
