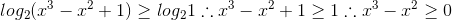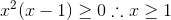Inequação logaritima
4 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Inequação logaritima
por isaabella.d Ter 27 Mar 2018, 08:38
É correto afirmar que o conjunto solução da inequação em x E R, expressa por log(x³-x²+1) na base2 > ou igual a 0, é:
01) [-1,0] U [1, + infinito[
02) [1, + infinito[
03) [0, + infinito[
04) [-1, 1]
05) ]-infinito, -1] U [1, + infinito[
obs.: Não to conseguindo fazer a condição de existência da inequação polinomial...
01) [-1,0] U [1, + infinito[
02) [1, + infinito[
03) [0, + infinito[
04) [-1, 1]
05) ]-infinito, -1] U [1, + infinito[
obs.: Não to conseguindo fazer a condição de existência da inequação polinomial...
isaabella.d- Padawan
- Mensagens : 71
Data de inscrição : 23/08/2016
Idade : 30
Localização : Vitória da Conquista
RodrigoA.S- Elite Jedi
- Mensagens : 449
Data de inscrição : 12/07/2017
Idade : 25
Localização : Nova Iguaçu
Re: Inequação logaritima
por viniciuspfaria Dom 01 Abr 2018, 16:33
Alguém me ajuda nessas?
A) 3*(log3X) + 5*log3X-2 ≤ 0
B) (log ½ X)² − 3 ⋅ log ½ X − 4 > 0
A) 3*(log3X) + 5*log3X-2 ≤ 0
B) (log ½ X)² − 3 ⋅ log ½ X − 4 > 0
viniciuspfaria- Iniciante
- Mensagens : 6
Data de inscrição : 31/03/2018
Idade : 33
Localização : São Paulo
Re: Inequação logaritima
por Elcioschin Dom 01 Abr 2018, 18:44
Infelizmente não podemos ajudar, pois sua última mensagem viola a Regra VI do fórum
Elcioschin- Grande Mestre
- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Tópicos semelhantes» Inequaçao Logaritima
» Inequaçao Logaritima
» Desigualdade logarítima
» Função Logarítima
» Função logaritima
» Inequaçao Logaritima
» Desigualdade logarítima
» Função Logarítima
» Função logaritima
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
