Hexágono não regular
3 participantes
Página 1 de 1
Hexágono não regular
por PedroSantos Sáb 13 Jan 2018, 22:33
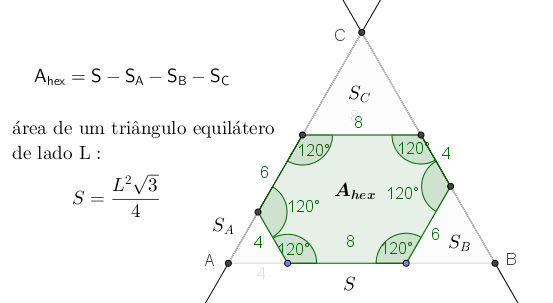
Um hexágono convexo é equiângulo e os seus lados medem 4m, 6m, 8m, sendo que lados opostos são congruentes. Determine a área desse hexágono.
Gab.: 52√3m²
Gab.: 52√3m²
PedroSantos- Iniciante
- Mensagens : 49
Data de inscrição : 25/05/2017
Idade : 22
Localização : Santo André
Re: Hexágono não regular
por Elcioschin Sáb 13 Jan 2018, 22:58
Desenhe o hexágono ABCDEFA com:
AB = DE = 4 ---> AF = BC = 6 ----> CD = EF = 8
A^BC = B^CD = C^DE = DÊF - E^FA = FÂB = 120º
Trace a diagonal CF e note que CF é paralela aos lados AB e DE.
Logo ABCF e DEFC são trapézios
No trapézio ABCF ---> A^FC = B^CF = 60º ---> trace as alturas h = AA' = BB'
A'ÂF = B'BC = 30º
h = AA' = AF.cos30º ---> h = 6.(√3/2) ---> h = 3.√3
A'F = AF.cos60º ---> A'F = 6.(1/2) ---> A'F = 3 ----> Similar ---> B'C = 3
CF = A'F + A'B' + B'C ---> CF = 10
Área deste trapézio : S' = (4 + 10).3.√3/2 ---> S' = 21.√3
Proceda de modo similar para o outro trapézio e achará H = 4.√3 . Calcule S"
S = S' + S"
AB = DE = 4 ---> AF = BC = 6 ----> CD = EF = 8
A^BC = B^CD = C^DE = DÊF - E^FA = FÂB = 120º
Trace a diagonal CF e note que CF é paralela aos lados AB e DE.
Logo ABCF e DEFC são trapézios
No trapézio ABCF ---> A^FC = B^CF = 60º ---> trace as alturas h = AA' = BB'
A'ÂF = B'BC = 30º
h = AA' = AF.cos30º ---> h = 6.(√3/2) ---> h = 3.√3
A'F = AF.cos60º ---> A'F = 6.(1/2) ---> A'F = 3 ----> Similar ---> B'C = 3
CF = A'F + A'B' + B'C ---> CF = 10
Área deste trapézio : S' = (4 + 10).3.√3/2 ---> S' = 21.√3
Proceda de modo similar para o outro trapézio e achará H = 4.√3 . Calcule S"
S = S' + S"
Elcioschin- Grande Mestre
- Mensagens : 71979
Data de inscrição : 15/09/2009
Idade : 77
Localização : Santos/SP
Re: Hexágono não regular
por Euclides Sáb 13 Jan 2018, 23:33
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.
Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.
Euclides- Fundador
- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
PedroSantos- Iniciante
- Mensagens : 49
Data de inscrição : 25/05/2017
Idade : 22
Localização : Santo André
Tópicos semelhantesPágina 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos|
|
|
