Canhão com triângulo

gabarito: V7 raiz quadrada de 7

Um canhão de luz está a 2m de distância de um painel retangular que possui um orifício triangular em sua superfície. Qual é a distância d necessária entre o canhão de luz e a parede para que a área do triângulo projetado fique 75% maior em relação ao orifício?

Seja S a área do triângulo menor

(d/2)² = 1,75.S/S

d²/4 = 1,75 ---> d² = 7 ---> d = √7

Obrigado, mestre.

Pelo que entendi, você usou a razão de semelhança e elevou as medidas lineares ao quadrado para igualar às de área, certo, Elcio?

O que eu não entendi é por que isso funciona. Isso não estaria relacionado à área dos triângulos coloridos abaixo? Nós queremos a área dos triângulos projetados.



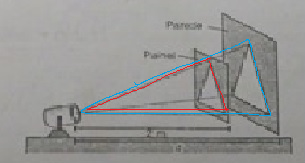
Por favor, poderia me explicar?

Obrigado

Sim foi exatamente isto que eu fiz

Isto é baseado num Teorema muito importante sobre homotetia e é muito aplicado em pirâmides e cones:

A relação entre duas áreas semelhantes é diretamente proporcional ao quadrado da relação entre medidas lineares semelhantes:

S/s = (D/d)²

A relação entre dois volumes semelhantes é diretamente proporcional ao cubo da relação entre medidas lineares semelhantes:

V/v = (D/d)³

Note, que na figura desta questão temos uma pirâmide maior e outra menor. As medidas lineares, neste caso são suas alturas (mas poderiam ser também os lados das bases)