Semelhança de triângulos (UFMG)
2 participantes
Página 1 de 1
Semelhança de triângulos (UFMG)
por Alisson Cabrini Qua 20 Set 2017, 15:34
(UFMG) Nesta figura, os ângulos ABC, CDE e EAB são retos, e os segmentos AD, CD e BC medem, respectivamente, x, y e z.
Nessa situação, a altura do triângulo ADE, em relação ao lado AE, é dada por:
Minha tentativa:
Já tenho os valores dos lados, agora encontrar a altura h?
Nessa situação, a altura do triângulo ADE, em relação ao lado AE, é dada por:
- R:
- B
Minha tentativa:
Já tenho os valores dos lados, agora encontrar a altura h?
Alisson Cabrini- Jedi
- Mensagens : 207
Data de inscrição : 22/05/2017
Idade : 28
Localização : Cordeirópolis-SP-Brasil
Re: Semelhança de triângulos (UFMG)
por Castiel Seg 25 Set 2017, 13:14
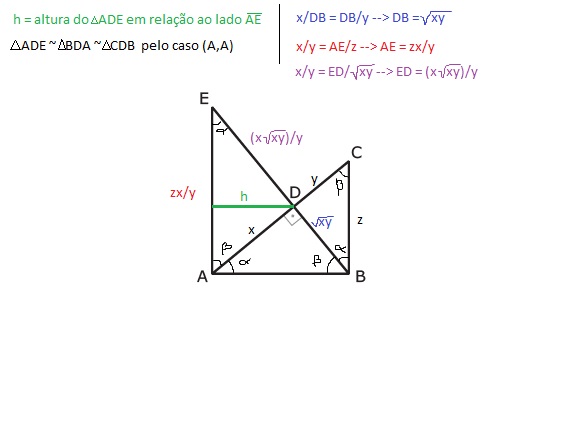
O triângulo ADE é retângulo, logo a área pode ser calculada por estas duas maneiras:
A = a.h/2 ----> H.(AE)/2 (altura relativa à hipotenusa x hipotenusa)/2
A = b.c/2 -----> (DE).(AD)/2 (semi produto dos catetos)
Agora, basta igualar:
H.(AE)/2 = (DE).(AD)/2
H.(AE) = (DE).(AD)
Agora, só resolver com os valores que você encontrou para esses segmentos.
(ou basta lembrar-se da relação métrica bc = ah )
A = a.h/2 ----> H.(AE)/2 (altura relativa à hipotenusa x hipotenusa)/2
A = b.c/2 -----> (DE).(AD)/2 (semi produto dos catetos)
Agora, basta igualar:
H.(AE)/2 = (DE).(AD)/2
H.(AE) = (DE).(AD)
Agora, só resolver com os valores que você encontrou para esses segmentos.
(ou basta lembrar-se da relação métrica bc = ah )
Castiel- Padawan
- Mensagens : 84
Data de inscrição : 04/06/2017
Idade : 24
Localização : Rio de Janeiro
Tópicos semelhantes» (UFMG-97) Observe a figura.... semelhança de triângulos e triângulos retângulos.
» (UFMG) - Semelhança de triângulos e triângulos retângulos.
» (UFMG) Semelhança de triângulos
» Semelhança de triângulos
» Semelhança de triangulos
» (UFMG) - Semelhança de triângulos e triângulos retângulos.
» (UFMG) Semelhança de triângulos
» Semelhança de triângulos
» Semelhança de triangulos
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
