Questão de Função Quadrática
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Questão de Função Quadrática
por zDudaH Ter 18 Jul 2017, 22:03
(Fatec 98) Sejam Va o conjunto verdade da equação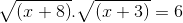 
e Vb o conjunto verdade da equação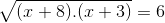
no conjunto universo dos Reais.
I. Va = Vb
II. Va ⊂ Vb
III. -12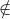
Va; 1 ∈ Va ∩ Vb; -12 ∈ Vb
É verdade que:
a) somente I é falsa
b) somente II é falsa
c) somente III é falsa
d) todas são verdadeiras
e) todas são falsas
Gabarito [A]
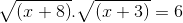
e Vb o conjunto verdade da equação
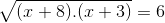no conjunto universo dos Reais.I. Va = Vb
II. Va ⊂ Vb
III. -12
É verdade que:
a) somente I é falsa
b) somente II é falsa
c) somente III é falsa
d) todas são verdadeiras
e) todas são falsas
Gabarito [A]
zDudaH- Iniciante
- Mensagens : 29
Data de inscrição : 03/05/2017
Idade : 25
Localização : São José, SC, Brasil
Re: Questão de Função Quadrática
por Elcioschin Ter 18 Jul 2017, 22:19
A) √(x + 8 ).√(x + 3) = 6 ---> Restrição: x > - 3
(x + 8 ).(x + 3) = 36 ---> x² + 11x - 12 = 0
Raízes ---> x = - 12 (não serve, pela restrição) e x = 1
B) √[(x + 8 ).(x + 3)] = 6 --> Restrição (x + 8 ).(x + 3) > 0 --> x² + 11.x + 24 > 0
Raízes da restrição ---> x = - 3 e x = - 8 ---> x < - 8 ou x > - 3
x² + 11.x + 24 = 36 ---> idem A
Complete
(x + 8 ).(x + 3) = 36 ---> x² + 11x - 12 = 0
Raízes ---> x = - 12 (não serve, pela restrição) e x = 1
B) √[(x + 8 ).(x + 3)] = 6 --> Restrição (x + 8 ).(x + 3) > 0 --> x² + 11.x + 24 > 0
Raízes da restrição ---> x = - 3 e x = - 8 ---> x < - 8 ou x > - 3
x² + 11.x + 24 = 36 ---> idem A
Complete
Elcioschin- Grande Mestre
- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Re: Questão de Função Quadrática
por MakiseKurisu Sáb 08 Ago 2020, 21:47
Essa questão é realmente intrigante. Me surgiu uma dúvida a respeito da propriedade da radiciação, que se refere à multiplicação de radicais com mesmo índice e mesma base. Ora, essa propriedade quer dizer, basicamente, que as duas equações do enunciado são iguais não? Se são iguais, como podem apresentar soluções diferentes? O que se pode concluir a partir dessa questão e da propriedade?Elcioschin escreveu:A) √(x + 8 ).√(x + 3) = 6 ---> Restrição: x > - 3
(x + 8 ).(x + 3) = 36 ---> x² + 11x - 12 = 0
Raízes ---> x = - 12 (não serve, pela restrição) e x = 1
B) √[(x + 8 ).(x + 3)] = 6 --> Restrição (x + 8 ).(x + 3) > 0 --> x² + 11.x + 24 > 0
Raízes da restrição ---> x = - 3 e x = - 8 ---> x < - 8 ou x > - 3
x² + 11.x + 24 = 36 ---> idem A
Complete
MakiseKurisu- Recebeu o sabre de luz
- Mensagens : 157
Data de inscrição : 15/03/2017
Idade : 25
Localização : Brasil-SC-Joinville
Re: Questão de Função Quadrática
por Elcioschin Dom 09 Ago 2020, 11:23
As duas equações NÃO são iguais. Veja porque:
x = √(-4).√(-4) ---> x = [√(4).√(-1)].[√(4).√(-1)] ---> x = (2.i).(2.i) --->
x = 4.i² ---> x = - 4
x = √[(-4).(-4)] ---> √(16) = √(4²) ---> x = 4
Isto significa que a Regra da multiplicação de radicais não vale sempre.
x = √(-4).√(-4) ---> x = [√(4).√(-1)].[√(4).√(-1)] ---> x = (2.i).(2.i) --->
x = 4.i² ---> x = - 4
x = √[(-4).(-4)] ---> √(16) = √(4²) ---> x = 4
Isto significa que a Regra da multiplicação de radicais não vale sempre.
Elcioschin- Grande Mestre
- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
MakiseKurisu gosta desta mensagem
Tópicos semelhantes» Questão de função quadrática
» QUESTÃO FUNÇÃO QUADRÁTICA
» Questão de função quadrática
» Questão de função quadrática
» Questão UFT Inversa Da Função Quadrática
» QUESTÃO FUNÇÃO QUADRÁTICA
» Questão de função quadrática
» Questão de função quadrática
» Questão UFT Inversa Da Função Quadrática
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
