(Enem 2016.3) Circunferências e reta tangente

por gptossin Qui 29 Jun 2017, 22:15

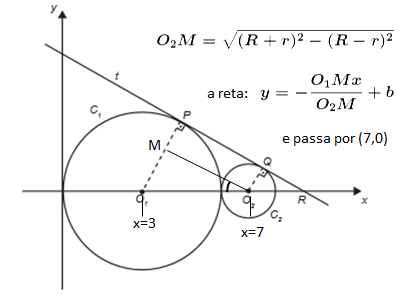
Na figura estão representadas, em um plano cartesiano, duas circunferências: C¹(de raio 3 e centro O¹) e C²(de raio 1 e centro O²), tangentes entre si, e uma reta t tangente às duas circunferências nos pontos P e Q.
(Enem 2016.3) Circunferências e reta tangente RB_AIQh5T1Gl8xuk3Wby5Q

(Enem 2016.3) Circunferências e reta tangente RB_AIQh5T1Gl8xuk3Wby5Q

Nessas condições, a equação da reta t é:

Postagem em desacordo com a Regra XI do fórum: não foram postadas as alternativas.

por **Euclides** Qui 29 Jun 2017, 22:31

por paulinhomesquita Seg 24 Jul 2017, 20:21

Ótima saída, Euclides. Só um detalhe: a reta t não passa pelo ponto (7,0).

por **Elcioschin** Ter 25 Jul 2017, 12:11

Basta fazer uma pequena correção

O₂M = √(4² - 2²) = 2.√3

O coeficiente angular da reta t e da reta O₂M vale: - O₁M/O₂M = - (R - r)/2.√3 = - 2/2.√3 = - √3/3

Isto significa que MÔ₂O₁ = 30º ---> Logo QÔ₂R = 60º

Seja Q' o pé da perpendicular de Q sobre o eixo x ---> O₂Q' = O₂Q.cosQÔ₂R ---> O₂Q' = 1.cos60º ---> O₂Q' = 1/2

QQ' = O₂Q.sen60º ---> QQ' = 1.(√3/2) ---> QQ' = √3/2

OQ' = OO₂+ O₂Q' = ---> OQ' = 7 + 1/2 ---> OQ' = 15/2 ----> Q(15/2, √3/2) ---> Ponto pelo qual passa a reta r

Basta agora calcular a equação da reta r

por Raissa18 Qua 27 Set 2017, 10:48

Essa parte do Q' nao entendi muito bem,voce poderia me mandar o desenho da imagem com esse ponto?

por **Elcioschin** Qua 27 Set 2017, 12:01

Q aparece na figura e o o eixo x também

Por Q trace uma reta perpendicular ao eixo x.
Seja Q' o ponto onde esta perpendicular intercepta o eixo x

No triângulo retângulo O₂Q'Q (reto em Q') podemos escrever

O₂Q' = O₂Q.cosQÔ₂Q' ---> O₂Q' = 1.cos60º ---> O₂Q' = 1/2

QQ' = O₂Q.cosQÔ₂Q' ---> QQ' = 1.sen60º ---> QQ' = √3/2

Note agora que:

QQ' é a ordenada do ponto Q ---> yQ
A abcissa do ponto Q é: xQ = OQ₂+ O₂Q' --> xQ = 7 + 1/2 ---> xQ = 15/2 ----> Q(15/2, √3/2)