Equação do 2° grau

O conjunto-solução da inequação 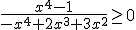 é

A) [img]http://www2.equacao.mat.br/latex/mimetex.cgi?]-\infty,-1[[/img]
B) [img]http://www3.equacao.mat.br/latex/mimetex.cgi?]-1,1[[/img]
C) [img]http://www2.equacao.mat.br/latex/mimetex.cgi?[1,3[[/img]
D) [img]http://www2.equacao.mat.br/latex/mimetex.cgi?[3,+\infty][/img]
E) [img]http://www3.equacao.mat.br/latex/mimetex.cgi?]-\infty,1]\cup]3,+\infty[[/img]


Obs: Gabarito letra C


Alguém pode me explicar o porquê do 3 ter que ser obrigatoriamente positivo?
Segue uma explicação que eu achei na net.
A parte de cima é fácil perceber que para  temos .

Na parte de baixo podemos fatorar: , onde é fácil perceber que isso é sempre negativo para qualquer . Como queremos sempre positivo, basta inverter a desigualdade e temos .

Unindo as soluções: 

Como a parte de baixo não pode ser zero pois causa uma indeterminação, tiramos a igualdade com  que resulta em zero.

Boa tarde, 

Me desculpe, mas não entendi a sua dúvida.

Acredito que essa solução que você encontrou na net está incompleta e até incorreta.

Como queremos que o quociente de dois números seja maior ou igual a zero, temos dois casos:

I) O caso em que tanto o numerador quanto o denominador são positivos:

x⁴ - 1 ≥ 0  e  -x²(x+1)(x-3) > 0

I.a) x⁴ - 1 ≥ 0   

x⁴ - 1 será maior ou igual a zero se x ≥ 1 ou se x ≤ -1

I.b) 

-x²(x+1)(x-3) > 0 

-x² sempre será negativo. 

Daí temos duas novas possibilidades para que o produto seja maior que zero:

i) x + 1 < 0  e  x - 3 > 0  

x < -1  e x > 3     impossível

ii) x + 1 > 0  e x - 3 < 0 

x > -1   e   x < 3         →     -1 < x < 3  (veja que sua solução afirma que a expressão será positiva para x ≤ 3, mas isso não é verdade. Para x = -2, por exemplo, teremos (-4).(-1).(-5) = - 20  )

Unindo I.a e I.b, temos que :  1 ≤ x < 3

II) O caso em que o numerador e o denomiador são negativos:

x⁴ - 1 ≤ 0  e  -x²(x+1)(x-3) < 0

II.a) x⁴ - 1 ≤ 0 

-1 ≤ x ≤ 1 

II.b) -x²(x+1)(x-3) < 0

-x² sempre será negativo.

Então, caímos em outros dois casos:

iii) x+1 > 0   e   x -3 > 0 
x > -1    e   x > 3   →   x > 3 

iiii) x + 1 < 0  e x-3 < 0 

x < -1   e   x < 3   →   x < 3 

Veja que unindo as possível soluções de II.a com II.b, não temos intersecções.

Logo a solução do problema é :  1  ≤ x < 3

Veja se ainda fica com dúvida e me avisa para que eu possa esclarecê-la.

Muito obrigada por me ajudar, mas porque na parte I.b-i é impossível a solução?

Sem problemas!

Pois é impossível que x seja menor que -1 e maior que 3 ao mesmo tempo.  :face:

Ahhh, agr entendi. Demorei um pouco pra entender a questão toda, mas consegui. Muito obrigada pela paciência e atenção.