Energia mecânica

(UFJF) As figuras I e II mostram dois casos de lançamento de uma mesma bola de massa m. Em ambas as situações, a bola se encontra próximo à superfície da Terra. Na figura I, a bola é lançada com vetor velocidade inicial v0 sobre um plano inclinado, sem atrito. Este faz um ângulo em relação à direção horizontal. Na figura II, a bola é lançada com o mesmo vetor velocidade inicial v0 , na mesma direção que a indicada na figura I. Desprezando a resistência do ar, para esses lançamentos, é correto afirmar que:

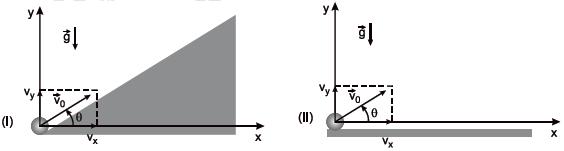
a) as alturas máximas em I e II são as mesmas.
b) nas alturas máximas, as energias potenciais em I e II são as mesmas.
c) nas alturas máximas, as energias mecânicas em I e II são as mesmas.
d) nas alturas máximas, a energia mecânica em I é nula e em II não.
e) nas alturas máximas, a energia mecânica em II é nula e em I não.

Fiquei entre a a) e a c). Alguém pode me ajudar, fazendo um favor??

Mera aplicação de fórmulas básicas:

I) Plano inclinado ---> Eci = (1/2).m.Vo² ----> Epf = m.g.H_máx  

Conservação de energia: Epf = Eci --> m.g.H_máx = (1/2).m.Vo² --> H_máx = Vo²/2.g

II) Lançamento oblíquo ---> Voy = Vo.senθ

Altura máxima: h_máx = Vo².sen²θ/2.g ---> h_máx = (Vo²/2.g).sen²θ

O que você acha, agora, da alternativa A?

Entendi. Obrigada!!!!

Uppp, alguém sabe me explicar por que a energia mecânica será a mesma?

brunamarc escreveu:Uppp, alguém sabe me explicar por que a energia mecânica será a mesma?

Porque não há a atuação de forças dissipativas em nenhum dos casos. Logo, a energia mecânica se conserva ao longo de todo o movimento de A e de B. Se ambos são lançados com mesma energia (que no caso é dada, no instante 0, pela energia cinética, e varia apenas com a massa e a velocidade, que são iguais em ambos os casos), então eles remanescerão com a mesma energia ao longo de todo o percurso do movimento. Isso valerá até o momento em que entrarem em contato com alguma força dissipativa, a exemplo de atrito com o solo, atrito com o vento ou inúmeras outras.

Obrigada, Christian!! )

Então a altura atingida, na condição do plano inclinado, será maior que na do lançamento oblíquo?

No plano inclinado: Hmáx = Vo²/2.g

No lançamento oblíquo: hmáx = (Vo²/2.g).sen²θ

Lembre-se que, no 1º quadrante --> 0 < senθ < 1

Compare ambas e diga o que você acha!

Nesse viés, creio estar confirmada a tese sugerida; muito obrigado, Elcio! <3