Teorema de tales.
2 participantes
Página 1 de 1
Teorema de tales.
por bulnoturno Dom 26 Mar 2017, 15:20
Boa tarde,
Estou com essa questão que infelizmente não tenho gabarito. Aparentemente simples, mas não consegui resolver. a//b//c//d. Pede-se x, y e z.
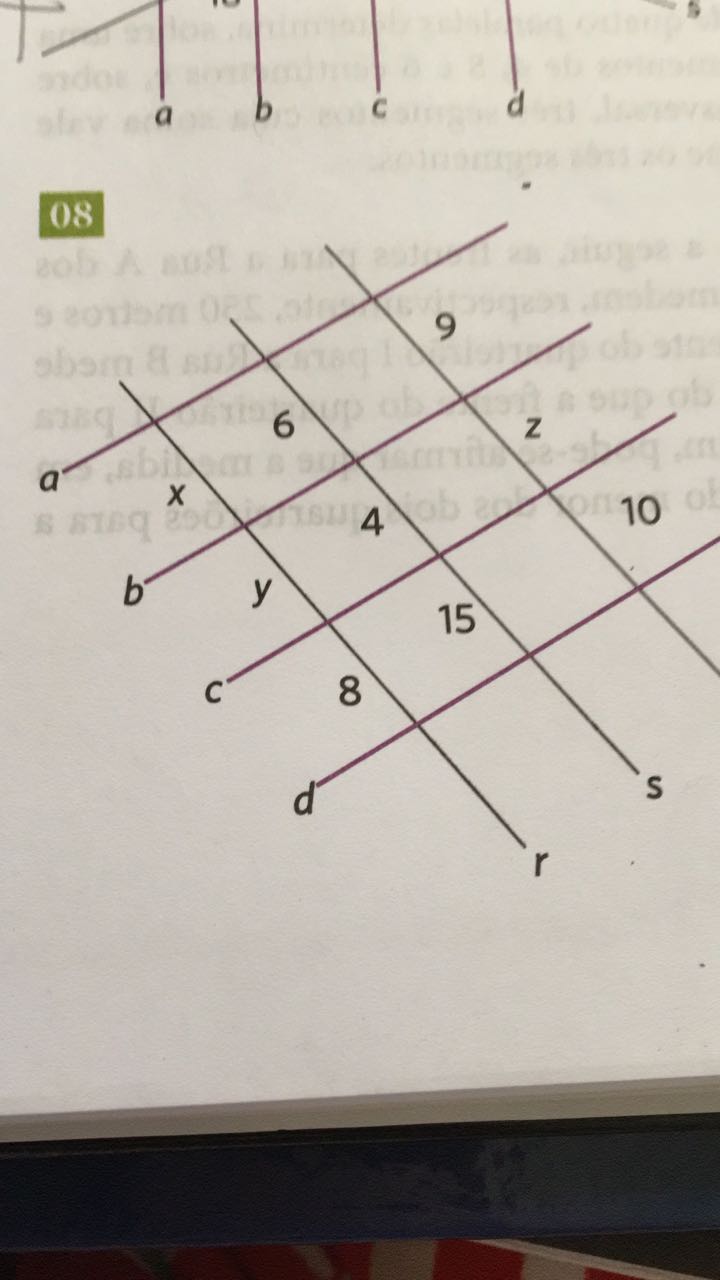
Estou com essa questão que infelizmente não tenho gabarito. Aparentemente simples, mas não consegui resolver. a//b//c//d. Pede-se x, y e z.
bulnoturno- Iniciante
- Mensagens : 17
Data de inscrição : 29/09/2016
Idade : 36
Localização : Colatina
Re: Teorema de tales.
por bulnoturno Dom 26 Mar 2017, 15:34
A unica forma que eu consegui resolver até agora foi se eu supor que estão invertidos o 6 e o 9. Até pq se esse não for o caso não faz sentido a posição do 6 com o 9 e o 15 com o 10.
Ai eu acho x = 72/15, z = 8/10 e y = 32/15.
Ai eu acho x = 72/15, z = 8/10 e y = 32/15.
bulnoturno- Iniciante
- Mensagens : 17
Data de inscrição : 29/09/2016
Idade : 36
Localização : Colatina
Re: Teorema de tales.
por Medeiros Dom 26 Mar 2017, 16:27
Concordo contigo, o '6' e o '2' estão em posições trocadas.
Sabemos, pelo enunciado, que {a, b, c, d} são paralelas entre si, porém não o são {r, s, t}. Mas, de qualquer forma, a proporcionalidade dos segmentos das concorrentes deve ser mantido. Assim,
-- como está, 6/9 = 15/10 é uma mentira;
-- já, como propuseste, 9/6 = 15/10 é o correto.
Obs.: também poderia ser invertido o '15' com o '10'.
Sabemos, pelo enunciado, que {a, b, c, d} são paralelas entre si, porém não o são {r, s, t}. Mas, de qualquer forma, a proporcionalidade dos segmentos das concorrentes deve ser mantido. Assim,
-- como está, 6/9 = 15/10 é uma mentira;
-- já, como propuseste, 9/6 = 15/10 é o correto.
Obs.: também poderia ser invertido o '15' com o '10'.
Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Tópicos semelhantesPágina 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
