Decomposição de número - Análise Combinatória
2 participantes
Página 1 de 1
 Decomposição de número - Análise Combinatória
Decomposição de número - Análise Combinatória
Boa tarde.
De quantos modos 324 pode ser decomposto em um produto de 2 inteiros positivos?
Obrigado desde já.
De quantos modos 324 pode ser decomposto em um produto de 2 inteiros positivos?
Obrigado desde já.
Mbssilva- Elite Jedi

- Mensagens : 359
Data de inscrição : 15/01/2015
Idade : 25
Localização : Paraná, Brasil
 Re: Decomposição de número - Análise Combinatória
Re: Decomposição de número - Análise Combinatória
162x2
108x3
81x4
54x6
36x9
27x12
18x18
Ao invés de pegar um a um e dividir, pode-se fazer o arranjo de fatores:
1->2, 3.
2->2x2, 2x3, 3x3.
3->2x2x3, 2x3x3, 3x3x3.
Repare que aqui há 8, mas contabilizei apenas 7, pois 3x3x3 dá 27 (já temos um termo assim (2x2x3 x 27).
-------------
Esqueci do 1x324.
108x3
81x4
54x6
36x9
27x12
18x18
Ao invés de pegar um a um e dividir, pode-se fazer o arranjo de fatores:
1->2, 3.
2->2x2, 2x3, 3x3.
3->2x2x3, 2x3x3, 3x3x3.
Repare que aqui há 8, mas contabilizei apenas 7, pois 3x3x3 dá 27 (já temos um termo assim (2x2x3 x 27).
-------------
Esqueci do 1x324.
Convidado- Convidado
 Re: Decomposição de número - Análise Combinatória
Re: Decomposição de número - Análise Combinatória
Minha dúvida era se o 18x18 entraria na contagem. Percebi que se pegar os termos equidistantes nos divisores organizados em ordem crescente e multiplica-los obtêm se o resultado. Mas com 324(que tem 15 divisores) eu estava com essa dúvida. Obrigado pela ajuda.
____________________________________________
Baixe o livro Análise Combinatória e Probabilidade do A.C. Morgado com o gabarito e o solucionário dos exercícios.
Link 1: https://drive.google.com/open?id=0B4rrFzh6MB34NlVpeEpMZEdYSWs
Link 2: https://mega.nz/#F!FcpEWTCC!XrlsFKcPNR3ePOFm3OVJsg
Mbssilva- Elite Jedi

- Mensagens : 359
Data de inscrição : 15/01/2015
Idade : 25
Localização : Paraná, Brasil
 Re: Decomposição de número - Análise Combinatória
Re: Decomposição de número - Análise Combinatória
É bom ter cuidado nesse tipo de exercício.
Se você contar todos os fatores que usei, notará que são 15 números.
Mas 2x168 e 168x2 são iguais, logo devem ser contados 1 vez. E 18x18 também uma.
Se você contar todos os fatores que usei, notará que são 15 números.
Mas 2x168 e 168x2 são iguais, logo devem ser contados 1 vez. E 18x18 também uma.
Convidado- Convidado
 Re: Decomposição de número - Análise Combinatória
Re: Decomposição de número - Análise Combinatória
Boa tarde,Mbssilva escreveu:Boa tarde.
De quantos modos 324 pode ser decomposto em um produto de 2 inteiros positivos?
Obrigado desde já.
324 = 2.2.3.3.3.3 = 2².3⁴
Número de divisores de 324 = (2+1)(4+1) = 3*5 = 15
Como os expoentes dos fatores primos são pares, significa que 324 é quadrado perfeito, cuja raiz é igual ao produto dos mesmos fatores primos, com expoentes iguais à metade:
2¹.3² = 2.9 = 18.
Assim, os produtos que podem ser formados, até o divisor 18 são:
1*324
2*162
3*108
4*81
6*54
9*36
12*27
18*18
São oito, portanto, os modos pelos quais 324 poderá ser separado em um produto de dois fatores positivos. Os outros sete são repetições destes (324*1, 162*2, etc).
Um abraço.

ivomilton- Membro de Honra

- Mensagens : 4994
Data de inscrição : 08/07/2009
Idade : 92
Localização : São Paulo - Capital
 Re: Decomposição de número - Análise Combinatória
Re: Decomposição de número - Análise Combinatória
Obrigado Ivomilton.
Obrigado Riobrancoabc.
Ivomilton, percebi que seu raciocínio foi diferente do riobrancoabc e agora fiquei na dúvida.
No caso do 648, como você faria por exemplo, já que ele não é um quadrado perfeito? Qual seria o divisor máximo que deveria ser atingido?? Porque antes eu resolvia apenas dividindo o número de divisores por 2. Aí surgiu a dúvida de como fazer isso num quadrado perfeito. Agora estou na dúvida de como aplicar seu raciocínio para um não quadrado perfeito. Não sei se fui muito claro :s
Obrigado Riobrancoabc.
Ivomilton, percebi que seu raciocínio foi diferente do riobrancoabc e agora fiquei na dúvida.
No caso do 648, como você faria por exemplo, já que ele não é um quadrado perfeito? Qual seria o divisor máximo que deveria ser atingido?? Porque antes eu resolvia apenas dividindo o número de divisores por 2. Aí surgiu a dúvida de como fazer isso num quadrado perfeito. Agora estou na dúvida de como aplicar seu raciocínio para um não quadrado perfeito. Não sei se fui muito claro :s
____________________________________________
Baixe o livro Análise Combinatória e Probabilidade do A.C. Morgado com o gabarito e o solucionário dos exercícios.
Link 1: https://drive.google.com/open?id=0B4rrFzh6MB34NlVpeEpMZEdYSWs
Link 2: https://mega.nz/#F!FcpEWTCC!XrlsFKcPNR3ePOFm3OVJsg
Mbssilva- Elite Jedi

- Mensagens : 359
Data de inscrição : 15/01/2015
Idade : 25
Localização : Paraná, Brasil
 Re: Decomposição de número - Análise Combinatória
Re: Decomposição de número - Análise Combinatória
Eu faria assim:
1)Decomponho em fatores primos.
648=(2^3).(3^4)
2)Número de divisores.
Nº=20.
Como ele não é um quadrado perfeito, não existe x^2=648.
Exemplificação para você pensar:
Se fosse um quadrado perfeito:
36-> 9 divisores.
1x36, 2x18, 3x12, 4x9, 6x6, 9x4, 12x3, 18x2, 36x1.
Se não fosse num quadrado perfeito:
72-> 12 divisores.
1x72, 2x36, 3x24, 4x18, 6x12, 8x9, 9x8, 12x6, 18x4, 24x3, 36x2, 72x1.
Olhe uma comparação com expansão binomial:
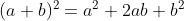
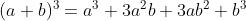
1)Decomponho em fatores primos.
648=(2^3).(3^4)
2)Número de divisores.
Nº=20.
Como ele não é um quadrado perfeito, não existe x^2=648.
Exemplificação para você pensar:
Se fosse um quadrado perfeito:
36-> 9 divisores.
1x36, 2x18, 3x12, 4x9, 6x6, 9x4, 12x3, 18x2, 36x1.
Se não fosse num quadrado perfeito:
72-> 12 divisores.
1x72, 2x36, 3x24, 4x18, 6x12, 8x9, 9x8, 12x6, 18x4, 24x3, 36x2, 72x1.
Olhe uma comparação com expansão binomial:
Convidado- Convidado
 Re: Decomposição de número - Análise Combinatória
Re: Decomposição de número - Análise Combinatória
No caso de ser 648 o número em pauta, procuraria determina sua raiz quadrada aproximada:Mbssilva escreveu:Obrigado Ivomilton.
Obrigado Riobrancoabc.
Ivomilton, percebi que seu raciocínio foi diferente do riobrancoabc e agora fiquei na dúvida.
No caso do 648, como você faria por exemplo, já que ele não é um quadrado perfeito? Qual seria o divisor máximo que deveria ser atingido?? Porque antes eu resolvia apenas dividindo o número de divisores por 2. Aí surgiu a dúvida de como fazer isso num quadrado perfeito. Agora estou na dúvida de como aplicar seu raciocínio para um não quadrado perfeito. Não sei se fui muito claro :s
648 = 324*2
√648 = √324*√2 = 18√2 = 18*1,4 = 25,2
Assim, listaria os divisores até um divisor igual ou menor que 25, e depois os contaria:
1*648
2*324
3*216
4*162
6*108
8*81
9*72
12*54
18*36
24*27
Seriam, então, dez os produtos de dois inteiros positivos. possíveis de serem formados.
Quando precisar listar todos os divisores de um número, poderá proceder assim:
Decomponha o número em seus fatores primos e o escreva na forma de um produto dos fatores primos encontrados com seus respectivos expoentes:
648 = 2³.3⁴
Quantidade de divisores positivos = (3+1)(4+1) = 4*5 = 20
Como o fator primo de maior expoente é o 3⁴, comece por ele, escrevendo em uma linha, todas as suas potências, a partir da potência zero:
1___3___9__27__81
Abaixo do 1, em coluna, escreva as potências do 2:
1___3___9__27__81
2
4
8
A seguir, multiplique o 2 por todos os elementos da linha anterior:
1___3___9__27__81
2___6__18__54_162
4
8
Continue, repetindo o mesmo processo com o 4 e o 8:
1___3___9__27__81
2___6__18__54_162
4__12__36_108_324
8__24__72_216_648
Conferindo a quantidade de divisores:
4 linhas x 5 colunas = 20
E assim temos todos eles:
1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72, 81, 108, 162, 216, 324, 648.
O par "24,27" é a parte central da lista.
Note que temos 9 divisores antes desse par e 9 divisores depois dele.
Um abraço.

ivomilton- Membro de Honra

- Mensagens : 4994
Data de inscrição : 08/07/2009
Idade : 92
Localização : São Paulo - Capital
 Re: Decomposição de número - Análise Combinatória
Re: Decomposição de número - Análise Combinatória
Entendi. Obrigado aos dois 
____________________________________________
Baixe o livro Análise Combinatória e Probabilidade do A.C. Morgado com o gabarito e o solucionário dos exercícios.
Link 1: https://drive.google.com/open?id=0B4rrFzh6MB34NlVpeEpMZEdYSWs
Link 2: https://mega.nz/#F!FcpEWTCC!XrlsFKcPNR3ePOFm3OVJsg
Mbssilva- Elite Jedi

- Mensagens : 359
Data de inscrição : 15/01/2015
Idade : 25
Localização : Paraná, Brasil
 Tópicos semelhantes
Tópicos semelhantes» Número de senhas em análise combinatória
» Número de Planos - Análise Combinatória
» Análise combinatória - (número de retas)
» Análise combinatória - (posição do número)
» Análise Combinatória - Fatorial de um número natural
» Número de Planos - Análise Combinatória
» Análise combinatória - (número de retas)
» Análise combinatória - (posição do número)
» Análise Combinatória - Fatorial de um número natural
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












