Equação modular

Eu queria saber qual a regra para se fazer equações modulares tipo essa |x-2|² + |x-5| -3 ,  tipo para t < 2 e para t<=2 x <5 e t>=5


qual seria a regra correta , para t<2 temos que fazer manter o primeiro modulo como está , e depois fazer |-(x-5)| -3 ?
 
ai para t<=2 x <5


temos que  multiplicar o sinal de menos nos dois modulos ............




eu queria saber o macete quando a equação modular soma dois modulos e também quando está subtraindo tipo | x-3 | - |x-4| .

Uma equação/inequação modular sempre tem um sinal = ou > ou < ou ≤ ou ≥
E o que seria a variável t já que a incógnita é x ?

Logo a sua questão NÃO á uma equação/inequação modular

1)As raízes da equação |x-2|² + |x-5| -3 tem :

para x<2:
(2-x)² + (5-x) -3 =0
x² - 5x + 6 = 0 -> raízes : x=2 ou x=3 -> não servem pois estamos supondo x<2

para 2≤ x < 5:
(x-2)² + (5-x) - 3 = 0
x² -5x + 6 = 0 -> raízes x=2 ou x=3


para x≥ 5:
(x-2)² + (x-5) -3 = 0
x² - 3x -4 = 0 -> raízes : x=4 ou x=-1 -> não servem pois estamos supondo x≥ 5 . Daí a resposta é tem 2 soluções .


Eu entendi tudo , o macete nessa questão era para x<2  a gente multiplica o menos nos dois modulos


e para 2 <=x <5 a gente multiplica o menos apenas no segundo módulo


e para x≥ 5 a gente deixa a equação como está sem multiplicar nada .




2)(UERJ) O volume de água em um tanque varia com o tempo de acordo com a seguinte equação:



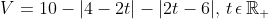
Nela, V é o volume medido em m^3 após t horas, contadas a partir de 8h de uma manhã. Determine os horários inicial e final dessa manhã em que o volume permanece constante.


Essa questão é para testar como anda os conhecimentos em função modular.

Vamos traçar a linha do tempo,






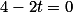
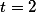
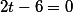
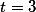
O que teremos que analisar é


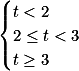
Para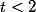  temos,
 V= 10 - (4-2T) - [-(2T-6)]



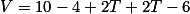
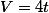
Para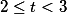  temos,
 V= 10-[-(4-2T)]-[-(2T-6)]



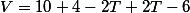
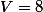
Para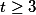  temos,
V=10 -[-(4-2T)] - (2T-6)



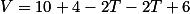
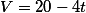
Veja que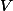  é constante apenas em 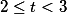, mas percebe que  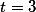temos,


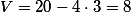
Pois no instante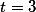  ele ainda está constante.

Desta forma os valores desejados são:



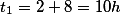
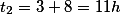
Valores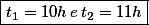 

Nessa questão o macete foi outro para T<2 ele multiplicou o segundo modulo por menos 

e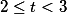   ele multiplicou por menos os dois módulos

e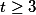  ele multiplicou por menos o primeiro módulo 




para soma o macete tem que ser igual o da primeira questão e para subtração tem que ser  igual o da segunda questão?? 
então na verdade existem macetes diferentes quando se soma faz de um jeito e quando subtrai faz de outro ?

Observe a definição de módulo de uma função



f(x) = | x | então:


| x | = | x  se  x >= 0
          | - x se x < 0