(CN1992) Numeros racionais e representação decimal

Seja M um conjunto cujos elementos são números naturais compostos por três algarismos distintos e primos absolutos. Sabe-se que o inverso de cada um deles é uma dízima periódica simples e que, invertendo-se a posição dos algarismos das centenas com os das unidades, em todos eles, os respectivos inversos são dízimas periódicas compostas. O número de subconjuntos de M é:
a)16
b)256
c)1024
d)2048
e)maior que 3000

Ajuda ae quem puder.
Obrigado.

Resolvido por Eduardo,

Toda dízima periódica simples pode ser escrita na forma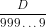 . Portanto, utilizando os números 2,3,5 e 7 para construir uma dízima simples o número não pode terminar com 2 e 5 pois: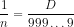, ou seja, 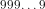é múltiplo de n, coisa que não é possível para um número terminado em 2 ou 5.

Portanto, apenas os números terminados em 3 ou 7 podem ser dízimas simples.

Pode-se provar que todo número da forma só é uma dízima composta se possuir 2 ou 5 como parte de seu fatoramento, ou seja, o número depois de invertido tem que terminar em 2 ou 5.

Portanto, os números que satisfazem as condições são:



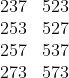
Com 8 elementos o número se subconjuntos é 2^n= 256.

Muito obrigado pela ajuda.

Primeiros devemos saber que os primos absolutos são 2, 3, 5 e 7
Então podemos formar 4 conjuntos compostos de 3 números primos absolutos, são eles:
{2,3,5}{2,3,7}{2,5,7}e{3,5,7}
E atraves destes 4 conjuntos podemos formar varios numeros
{2,3,5}{2,3,7}{2,5,7}e{3,5,7}
235 237 257 357
253 273 275 375
325 327 527 537
352 372 572 573
523 723 725 735
532 732 752 753

Para um numero ser uma dizima periodica sua fração irredutivel deve ter como denominador um numero primo que não seje 2 e/ou 5
Com isso podemos eliminar os números terminados em 2 e 5 pois se pegarmos seus inversos o denominador vai conter 2 e/ou 5 então os numeros quue irão sobrar são:
253, 523, 237, 273, 327, 723, 257, 527, 357, 537, 573 e 753.
Para um neumero ser dizima periodica composta sua fração irredutivel tem como denominador um primo qualquer mais 2 e/ou 5
Invertendo o algarismo das unidades pelo os das centenas os numeros:
327, 723, 357 e 753 ficarão terminados em 3 e 7 portanto o denominador de seu inverço não sera divisivel por 2 e 5 não sendo devido a isso uma dizima periodica composta
Então tambem podemos eliminar estes numeros sobrando apenas os numeros 253, 523, 237, 273, 257, 527, 537 e 573.
Com isso concluimos que o conunto M tem 8 elementos e como o numero de subconjuntos de certo conjunto é 2 elevado ao numeros de elementos desse conjunto o conjunto M tem 256 subconjuntos 2 elevado a oito.

Letra B

Conceito: para que haja uma dizima periódica simples deve haver fatores diferentes de 2 e/ou 5.

Conceito: para que haja uma dizima periódica composta deve haver fatores 2 e/ ou 5 juntamente com fatores diferentes desses.

Como nosso amigo de cima falou os únicos primos absolutos são: 2,3,5 e 7.

Diante da teoria deduzimos que c pode ser 3 e 7, novamente, b pode ser 2,3,5 e 7, pois ele não alterá na conclusão da dizima, e o a deve ser 2 ou 5. Juntando todas essas possibilidades formaremos 8 números, os quais são: 273,253,573,523,237,257,537,527. O numero de subconjuntos se da por 2^n=256.