EFOMM
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 EFOMM
EFOMM
Analise as afirmativas abaixo, sendo Z ∈ ¢
I. Se
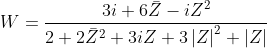
então podemos afirmar que
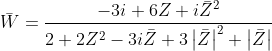
II. Dado |Z - 3i | podemos afirmar que é uma circunferência de centro (0,3) e raio 2
III. A forma trigonometrica de Z=6i é
)
IV.Sabe-se que -1 é raiz dupla da equação P(X)=2X4+X3-3X2-X+1 .logo,as outras raízes são números inteiros
Pode-se afirma que:
A)As afirmativas I e IV são verdadeiras
B)Apenas a afirmativa I é verdadeira
C)AS afirmativas II e IV são falsas
D)AS afirmativas I e II são verdadeiras
E)Apenas a afirmativa II é falsa
Pessoal desculpa pelo tamanho da questão,não é preguiça de fazer é duvida mesmo(Principalmente na I e II),ajuda por favor
Atentar para barrinhas acima dos números na I pois elas representam o conjugado
I. Se
então podemos afirmar que
II. Dado |Z - 3i | podemos afirmar que é uma circunferência de centro (0,3) e raio 2
III. A forma trigonometrica de Z=6i é
IV.Sabe-se que -1 é raiz dupla da equação P(X)=2X4+X3-3X2-X+1 .logo,as outras raízes são números inteiros
Pode-se afirma que:
A)As afirmativas I e IV são verdadeiras
B)Apenas a afirmativa I é verdadeira
C)AS afirmativas II e IV são falsas
D)AS afirmativas I e II são verdadeiras
E)Apenas a afirmativa II é falsa
Pessoal desculpa pelo tamanho da questão,não é preguiça de fazer é duvida mesmo(Principalmente na I e II),ajuda por favor
Atentar para barrinhas acima dos números na I pois elas representam o conjugado
- Gabarito :
- Letra D

jonathas.jbr- Padawan

- Mensagens : 97
Data de inscrição : 12/05/2016
Idade : 26
Localização : Rio de Janeiro
 Re: EFOMM
Re: EFOMM
I) Correto. Conjugado é o oposto da parte imaginária de um número complexo e segue algumas propriedades que foram respeitadas. Onde tem "i" fica "-i" e onde tem 
II) Correto. Ficou faltando a parte em negrito -> |Z-3i|=2. Elevar os 2 membros ao quadrado tornaria fácil a visualização. Sabendo que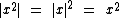 , então:
, então:
Equação reduzida da circunferência=(x-xc)2+(y-yc)2=r2
*A parte imaginária representa no plano de Argand-Gauss o eixo das ordenadas.
(z-3i)2=22 -->C(0,3) e r=2
Veja essa link que explica com mais detalhe:
Link
III) Errado. Onde tem cosseno era para estar o seno e vice-versa.
z=6i ; z=a+bi --> a=0 e b=6
|z|=√02+62
|z|=6
sen θ=b/|z|
sen θ=6/6=1
cos θ=a/|z|
cos θ=0/6=0
θ=π/2
z=|z|.(cos θ+isen θ)
z=6.(cos π/2+isen π/2)
IV) Errado. Sendo P(x)=2x4+x3-3x2-x+1 com x=-1 sendo raiz dupla temos que:
Relações de girard (esse cara te salva)
I)x1+x2+x3+x4=-b/a
-1-1+x3+x4=-1/2
x3+x4=-1/2+2
x3=3/2-x4
II)x1.x2.x3.x4=e/a
(3/2-x4).x4=1/2
-x42+(3/2).x4-1/2=0
∆=9/4-4.(-1).(-1/2)=0
∆=9/4-2
∆=1/4
x4=(-3/2±1/2)/-2
x'4=1/2(uma das raízes e não é número inteiro) e x''4=2 (não convém)
*substitua na fórmula e iguale a zero para saber se é raiz.

II) Correto. Ficou faltando a parte em negrito -> |Z-3i|=2. Elevar os 2 membros ao quadrado tornaria fácil a visualização. Sabendo que
Equação reduzida da circunferência=(x-xc)2+(y-yc)2=r2
*A parte imaginária representa no plano de Argand-Gauss o eixo das ordenadas.
(z-3i)2=22 -->C(0,3) e r=2
Veja essa link que explica com mais detalhe:
Link
III) Errado. Onde tem cosseno era para estar o seno e vice-versa.
z=6i ; z=a+bi --> a=0 e b=6
|z|=√02+62
|z|=6
sen θ=b/|z|
sen θ=6/6=1
cos θ=a/|z|
cos θ=0/6=0
θ=π/2
z=|z|.(cos θ+isen θ)
z=6.(cos π/2+isen π/2)
IV) Errado. Sendo P(x)=2x4+x3-3x2-x+1 com x=-1 sendo raiz dupla temos que:
Relações de girard (esse cara te salva)
I)x1+x2+x3+x4=-b/a
-1-1+x3+x4=-1/2
x3+x4=-1/2+2
x3=3/2-x4
II)x1.x2.x3.x4=e/a
(3/2-x4).x4=1/2
-x42+(3/2).x4-1/2=0
∆=9/4-4.(-1).(-1/2)=0
∆=9/4-2
∆=1/4
x4=(-3/2±1/2)/-2
x'4=1/2(uma das raízes e não é número inteiro) e x''4=2 (não convém)
*substitua na fórmula e iguale a zero para saber se é raiz.
EsdrasCFOPM- Estrela Dourada

- Mensagens : 1247
Data de inscrição : 22/02/2016
Idade : 30
Localização : Salvador, Bahia, Brasil
Lucas_DN684 gosta desta mensagem
 Re: EFOMM
Re: EFOMM
Entendi !!
Muito Obrigado resolução super completa !!!
Muito Obrigado resolução super completa !!!

jonathas.jbr- Padawan

- Mensagens : 97
Data de inscrição : 12/05/2016
Idade : 26
Localização : Rio de Janeiro
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












