Atrito em grãos

por Muá Qua 18 maio 2016, 19:20

De um ponto O, através de canais, situados num plano vertical, que formam diferentes ângulos com a vertical, simultaneamente começam a deslizar grãos de areia. O lugar geométrico dos pontos, nos quais se encontram os grãos de areia, é uma circunferência com centro que varia de posição com o tempo t.

Se o coeficiente de atrito entre um grão e o canal é u, o raio da circunferência no tempo t é:

A)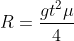 $Atrito em grãos Gif$
B)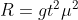 $Atrito em grãos Gif$
C)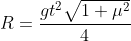 $Atrito em grãos Gif$
D)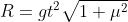 $Atrito e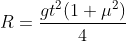m grãos Gif$
E) $Atrito em grãos Gif$

Não consegui visualizar sequer a situação.

por **gilberto97** Qui 19 maio 2016, 11:27

A situação é a seguinte: Cada grão pode ser imaginado como um bloco de massa m que desce um "plano inclinado". Imagine vários grãos e vários "planos". Em um plano inclinado com atrito, agem as seguintes forças:

Atrito em grãos Plano-inclinado-2

Sendo assim, como o grão desce (consegue se movimentar, logo o atrito é dinâmico), pela segunda lei de Newton:

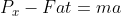
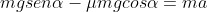
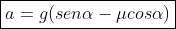
$Atrito em grãos Gif$

$Atrito em grãos Gif$

$Atrito em grãos Gif$

Da expressão acima para a aceleração, veja que quanto maior for o ângulo, maior também será a aceleração e quanto menor o ângulo, menor a aceleração. Podemos imaginar a seguinte configuração:

Atrito em grãos E0mywn

Veja que a cada instante muda a circunferência que passa pelos pontos/grãos naquele instante.

Temos que provar isso. Para a aceleração que encontramos, existe uma projeção vertical e outra horizontal. Ambas podem ser encontradas em função de $Atrito em grãos Gif$ , visto que formam um triângulo de vetores.

Atrito em grãos 2hfl2m9

Da trigonometria, segue que

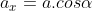
$Atrito em grãos Gif.latex?a_%7Bx%7D%3Da$

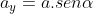$Atrito em grãos Gif.latex?a_%7By%7D%3Da$ .

Devido a essas acelerações, um grão irá deslocar-se tanto na direção x como na direção y. Trabalharei com x, mas é possível trabalhar com y, o resultado será o mesmo!

A velocidade inicial de cada grão é nula, assim a expressão para o deslocamento é

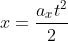
$Atrito em grãos Gif$

Para um determinado ponto P(x;y), onde encontra-se um grão qualquer, vale a seguinte relação:

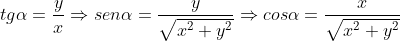
$Atrito em grãos Gif$

Então, a aceleração na direção horizontal, em função de x e y, será

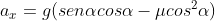
$Atrito em grãos Gif$

Substituindo as relações anteriores:

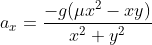
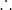
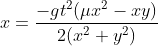
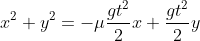
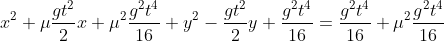
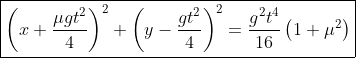
$Atrito em grãos Gif$

$Atrito em grãos Gif$

$Atrito em grãos Gif$

$Atrito em grãos Gif$

$Atrito em grãos Gif$

$Atrito em grãos Gif$

A equação acima é de uma circunferência cujo centro varia com o tempo, assim como seu raio, dado por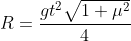 $Atrito em grãos Gif$ . Alternativa C.

EDIÇÃO: O centro da circunferência acima está no segundo quadrante. No entanto, existem outras circunferências cujos centros estão no quarto quadrante. Essas SIM são o lugar geométrico citado. A verdadeira equação geral é a seguinte:

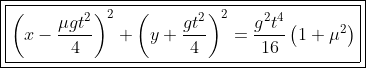
$Atrito em grãos Gif$

Note que a primeira equação iria satisfazer totalmente se os grãos terminassem a trajetória no ponto O. Como é em O que eles começam, o lugar geométrico desses grãos é simétrico ao primeiro.

Obs: Isso não afeta diretamente a questão em si, visto que ele pede apenas o raio da circunferência em função do tempo t.

por Muá Qui 19 maio 2016, 18:42

Não entendi o porque do seno e do cosseno serem negativos. Poderia explicar, por favor?

por **Ashitaka** Qui 19 maio 2016, 21:52

Na verdade, tanto faz se você os toma como positivo ou negativo e isso é nítido quando se joga na expressão de ax.
Esse exercício é muito interessante; de onde tirou-o?

por **gilberto97** Sex 20 maio 2016, 00:44

Muá escreveu:Não entendi o porque do seno e do cosseno serem negativos. Poderia explicar, por favor?

Como já foi dito acima, tanto faz. Se você considerar os valores de x e y em módulo, utilize o +, pois o ângulo alfa está no primeiro quadrante (seno, cosseno e tangente positivos). Vou fazer uma edição para não confundir.