Geometria plana ESPM

por Carbonila Sáb 14 maio 2016, 18:29

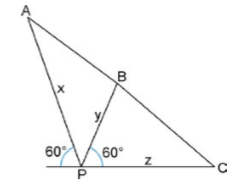
(ESPM) Na figura a seguir, os pontos A,B e C estão alinhados. Se PA=x, PB=y e PC=z, podemos afirmar que:
Geometria plana ESPM Mschf5

a) y=1/x+z
b) y=x+z/2
c)y² = x+z
d)1/y = 1/x + 1/z
e)z= xy/x+y

Gabarito:

por **Elcioschin** Sáb 14 maio 2016, 19:12

Vou dar as dicas

1) A^PB = 60º
2) Seja β = A^BP ---> C^BP = 180º - β
3) PÂB + A^PB + A^BP = 180º ---> PÂB + 60º + β = 180º ---> PÂB = 120º - β
4) P^CB + P^BC + B^PC = 180º ---> P^CB + (180º - β) + 60º = 180º --->
P^CB = β - 60º

Lei dos senos nos triângulos PAB e PCB

x/senβ = y/sen(120º - β)

z/sen(180º - β) = y/sen(β - 60º)

A parir dai é Trigonometria: sen(a - b) e Álgebra ---> Tente eliminar β

por **raimundo pereira** Sáb 14 maio 2016, 19:17

outro modo.
Geometria plana ESPM 25s7o5y

por **ivomilton** Sáb 14 maio 2016, 19:30

Carbonila escreveu:(ESPM) Na figura a seguir, os pontos A,B e C estão alinhados. Se PA=x, PB=y e PC=z, podemos afirmar que:

a) y=1/x+z
b) y=x+z/2
c)y² = x+z
d)1/y = 1/x + 1/z
e)z= xy/x+y
Gabarito:

Boa noite, Carboniia.

Ver Teorema 7, clicando no link abaixo:

http://www.obm.org.br/export/sites/default/semana_olimpica/docs/2013/geometria_cicero.pdf

....... 2.x.z.cos 60°
y = ------------------
............ x + z

...... 2.x.z.(1/2)
y = --------------
.......... x + z

......... xz
y = ---------
....... x + z

Invertendo cada membro, fica:

1 .... x + z
-- = --------
y .......xz

1 .... 1 .... 1
-- = --- + ---
y .... x .... z

Alternativa (D)

Um abraço.

por **Medeiros** Sáb 14 maio 2016, 22:34

Como de hábito o Raimundo nos oferece a mais rápida, criativa e melhor solução. Mas, só para acrescentar respostas, vou apresentar outro modo.

Geometria plana ESPM 24euet4

por **Medeiros** Sáb 14 maio 2016, 22:47

O teorema que o Ivo nos traz é a medida do comprimento da bissetriz de um triângulo qualquer conhecido o ângulo onde imbica a bissetriz e a medida dos seus lados. Há um bom tempo atrás mostrei isso aqui no fórum durante resolução de uma questão.

Fica mais fácil de memorizar se for enunciado assim: