ESPM- Geometria Plana
2 participantes
Página 1 de 1
ESPM- Geometria Plana
por Lord Stark Seg 04 Set 2017, 04:00
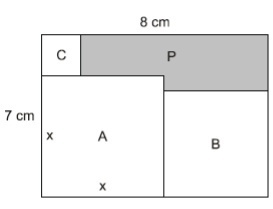
(Espm 2012) A figura abaixo mostra um retângulo de lados 7 cm e 8 cm no qual estão
contidos os quadrados A, B e C. A medida x pode variar entre 3,5 cm e 7 cm, fazendo com que
os lados dos três quadrados se alterem. Dentro desse intervalo, o maior valor que a
área do polígono P pode ter é igual a:
a) 18 cm2
b) 15 cm2
c) 17 cm2
d) 19 cm2
e) 16 cm2
Gab:A
contidos os quadrados A, B e C. A medida x pode variar entre 3,5 cm e 7 cm, fazendo com que
os lados dos três quadrados se alterem. Dentro desse intervalo, o maior valor que a
área do polígono P pode ter é igual a:
a) 18 cm2
b) 15 cm2
c) 17 cm2
d) 19 cm2
e) 16 cm2
Gab:A
Lord Stark- Jedi
- Mensagens : 218
Data de inscrição : 16/07/2017
Idade : 27
Localização : Caxias-MA
Re: ESPM- Geometria Plana
por Hikimaru Seg 04 Set 2017, 08:41
Área total = 7 . 8 = 56cm²
Área de A = x²
Área de B = (8 - x)² = 64 - 16x + x²
Área de C = (7 - x)² = 49 - 14x + x²
A área do polígono P é a área total menos a soma das áreas de A, B e C. Somando as três áreas: 3x² - 30x + 113
Portanto, área de P = 56 - (3x² - 30x + 113) = -3x² + 30x - 57
X do vértice = -b/2a => Xv = -30 / -6 = 5
Ou seja, o valor da área de P é máximo quando x for igual a 5. Voltando nas áreas:
Área de A = x² = 25
Área de B = (8 - x)² = 9
Área de C = (7 - x)² = 4
Portanto:
Ap = 56 - (25 + 9 + 4) = 56 - 38
Ap = 18cm²
Área de A = x²
Área de B = (8 - x)² = 64 - 16x + x²
Área de C = (7 - x)² = 49 - 14x + x²
A área do polígono P é a área total menos a soma das áreas de A, B e C. Somando as três áreas: 3x² - 30x + 113
Portanto, área de P = 56 - (3x² - 30x + 113) = -3x² + 30x - 57
X do vértice = -b/2a => Xv = -30 / -6 = 5
Ou seja, o valor da área de P é máximo quando x for igual a 5. Voltando nas áreas:
Área de A = x² = 25
Área de B = (8 - x)² = 9
Área de C = (7 - x)² = 4
Portanto:
Ap = 56 - (25 + 9 + 4) = 56 - 38
Ap = 18cm²
Hikimaru- Iniciante
- Mensagens : 30
Data de inscrição : 03/05/2017
Idade : 26
Localização : Jundiaí, SP - Brasil
cristhoferaspm e claralirasll gostam desta mensagem
Re: ESPM- Geometria Plana
por Lord Stark Ter 05 Set 2017, 20:53
Obrigado pela ótima explicação Hikimaru.
Lord Stark- Jedi
- Mensagens : 218
Data de inscrição : 16/07/2017
Idade : 27
Localização : Caxias-MA
Tópicos semelhantes» Geometria plana ESPM
» ESPM 2019 GEOMETRIA PLANA
» Questão geometria ESPM
» Geometria Plana
» Geometria Plana
» ESPM 2019 GEOMETRIA PLANA
» Questão geometria ESPM
» Geometria Plana
» Geometria Plana
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
