Equações Irracionais

por DiegoLima Seg 25 Abr 2016, 16:38

(ADVISE) Resolvendo-se a equação √4-3√10-3x = x-2 podemos afirmar que:

A) Não possui solução real.
B) Possui uma única solução real.
C) Possui duas soluções reais.
D) Possui três soluções reais.
E) Possui quatro soluções reais.

obs 1: 4-3√10 - 3x estão todos no radicando do primeiro radical

obs 2: A resposta correta é a letra B.

Desde já agradeço pela solução.

por **Claudir** Seg 25 Abr 2016, 18:14

Elevando ao quadrado duas vezes chegaremos à seguinte equação:

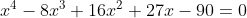
$x^4-8x^3+16x^2+27x-90=0$

Por inspeção, vemos que -2 é uma raíz.

Aplicando o algoritmo de Briot-Ruffini (ou dividindo a equação por x+2), obtemos:

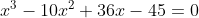
$x^3-10x^2+36x-45=0$

Novamente por inspeção, temos que 3 é uma raíz.

Reduzindo novamente o grau, encontraremos:

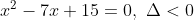
$x^2-7x+15=0,\ \Delta <0$

Como ∆ é menor que zero, ambas as raízes são imaginárias.

A equação inicial pode ser reescrita dessa forma:

$(x+2)(x-3)(x^2-7x+15)=0$

Temos 2 raízes reais e 2 imaginárias.

Todavia, há duas restrições iniciais que íamos deixando passar batido.

Algo dentro de uma raíz quadrada deve ser maior ou igual a zero para que seja real, portanto:

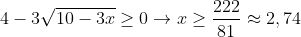
$4-3\sqrt{10-3x}\geq 0\to x\geq \frac{222}{81}\approx 2,74$

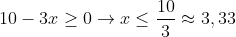
$10-3x\geq 0\to x\leq \frac{10}{3}\approx 3,33$

x = -2 não atende as condições estabelecidas acima, portanto, há apenas uma raíz real que satisfaça o enunciado (x = 3).

Equações Irracionais

Equações Irracionais

Re: Equações Irracionais

Um fórum livre e democrático.