Austrália - Números Complexos

por Lord Mentha Dom 10 Abr 2016, 16:18

"
Seja S = cotg^10(20º) + cotg^10(40º) + cotg^10(80º). Então o valor de 3.S é igual a?
A)22
B)23
C)24
D)25
E)26
"

Resposta:

Se alguém conseguir resolver essa aí, eu agradeço!

por **fantecele** Qua 30 Jan 2019, 23:46

É fácil reparar que os ângulos da forma 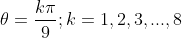$\\\theta=\frac{k\pi}{9};k=1,2,3,...,8$ , satisfazem a relação sen(9θ) = 0.

Utilizando números complexos podemos encontrar uma expressão para sen(9θ):

$\small \\(cos(\theta)+isen(\theta))^9=\binom{9}{0}(cos(\theta))^9+\binom{9}{1}(cos(\theta))^8(isen(\theta))^1+...+\binom{9}{9}(isen(\theta))^9\\cos(9\theta)+isen(9\theta)=\binom{9}{0}(cos(\theta))^9+\binom{9}{1}(cos(\theta))^8(isen(\theta))^1+...+\binom{9}{9}(isen(\theta))^9$

Igualando as partes imaginárias:

$\small \\sen(9\theta)=\binom{9}{1}(cos(\theta))^8(sen(\theta))-\binom{9}{3}(cos(\theta))^6(sen(\theta))^3+\binom{9}{5}(cos(\theta))^4(sen(\theta))^5-\\\binom{9}{7}(cos(\theta))^2(sen(\theta))^7+\binom{9}{9}(sen(\theta))^9$

Portanto, temos que os ângulos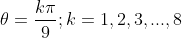 $\\\theta=\frac{k\pi}{9};k=1,2,3,...,8$ satisfazem a relação:

$\small \\\binom{9}{1}(cos(\theta))^8(sen(\theta))-\binom{9}{3}(cos(\theta))^6(sen(\theta))^3+\binom{9}{5}(cos(\theta))^4(sen(\theta))^5-\\\binom{9}{7}(cos(\theta))^2(sen(\theta))^7+\binom{9}{9}(sen(\theta))^9=0$

Sendo sen(θ) ≠ 0, podemos dividir a expressão acima por (sen(θ))^9, dessa forma iremos obter:

$\small \\\binom{9}{1}(cotg(\theta))^8-\binom{9}{3}(cotg(\theta))^6+\binom{9}{5}(cotg(\theta))^4-\binom{9}{7}(cotg(\theta))^2+\binom{9}{9}=0\\9.(cotg(\theta))^8-84.(cotg(\theta))^6+126.(cotg(\theta))^4-36.(cotg(\theta))^2+1=0\\9.(cotg^2(\theta))^4-84.(cotg^2(\theta))^3+126.(cotg^2(\theta))^2-36.(cotg^2(\theta))+1=0\,\,\,\,(I)$

Agora, perceba que $\small \\cotg^2\left (\frac{\pi}{9} \right )=cotg^2\left (\frac{8\pi}{9} \right )$ , valendo a mesma relação para os outros ângulos. Como temos que os ângulos θ para k igual a 1, 2, 3, 4 satisfazem (I), podemos considerar que $\small \\cotg^2\left (\frac{\pi}{9} \right ),cotg^2\left (\frac{2\pi}{9} \right ),cotg^2\left (\frac{3\pi}{9} \right ),cotg^2\left (\frac{4\pi}{9} \right )$ são raízes da seguinte equação:

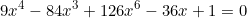
$\small \\9x^4-84x^3+126x^6-36x+1=0$

Considerando agora:

$\small \\S_n=\left (cotg^2\left (\frac{\pi}{9} \right ) \right )^n+\left (cotg^2\left (\frac{2\pi}{9} \right ) \right )^n+\left (cotg^2\left (\frac{3\pi}{9} \right ) \right )^n+\left (cotg^2\left (\frac{4\pi}{9} \right ) \right )^n$

Alguns valores simples de calcular são S2 = 532/9, S1 = 28/3, S0 = 4, S(-1) = 36, agora, por somas de Newton, podemos encontrar mais valores, sendo eles S3 = 11692/27, S4 = 263332/81, S5 = 5957308/243, dessa forma, temos que:

$\small \\(cotg(20))^{10}+(cotg(40))^{10}+(cotg(60))^{10}+(cotg(80))^{10}=\frac{5957308}{243}\\S=(cotg(20))^{10}+(cotg(40))^{10}+(cotg(80))^{10}=\frac{5957308}{243}-(cotg(60))^{10}\\\\S=(cotg(20))^{10}+(cotg(40))^{10}+(cotg(80))^{10}=\frac{5957308}{243}-\frac{1}{243}\\\\S=(cotg(20))^{10}+(cotg(40))^{10}+(cotg(80))^{10}=\frac{73547}{3}$

Dessa forma podemos encontrar o valor de 3S que é igual a 73547.
Creio que devemos calcular a soma dos algarismos de 3S, e assim podemos chegar ao valor 26, que corresponde a resposta dada.

Austrália - Números Complexos

Austrália - Números Complexos

Re: Austrália - Números Complexos

Um fórum livre e democrático.