UFRGS - função

por Erudonn Ter 23 Fev 2016, 20:40

(UFRGS) Considere o gráfico abaixo, que representa uma função polinomial f, de terceiro grau e domínio R.

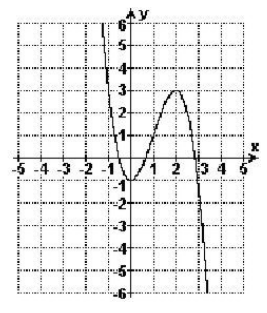
UFRGS - função V6is0y

Sendo g(x) = f(x) – 5, o número de raízes da equação g(x) = 0 é:
A) 0
B) 1
C) 2
D) 3
E) 4

por **Jader** Ter 23 Fev 2016, 20:44

g(x) ser igual a zero significa dique que

f(x) -5=0
f(x)=5

Evpelo gráfico de f(x) só tem um único valor que a função assume o valor 5.

Logo, g(x) só possui um único valor que à anula,ou seja, uma única raiz.

por Erudonn Ter 23 Fev 2016, 21:00

Obrigado pela ajuda Jader!

por **Elcioschin** Ter 23 Fev 2016, 22:03

Outro modo

Desloque o gráfico de f(x) 5 unidades para baixo

Com isto o vértice V(2, 3) passará a valer V'(2, - 2)

Com isto a única raiz será negativa (-2 < x < -1)

Isto significa que as outras duas raízes de g(x) são complexas