Questão Trigonometria

por gdo7701 Dom Fev 21 2016, 15:23

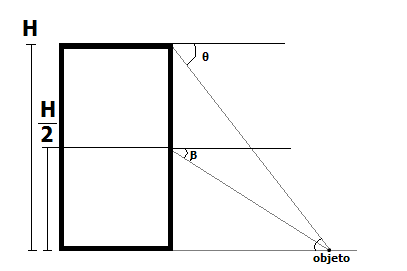
Do terraço de um edifício, representado a seguir (Spoiler Imagem), observa-se um objeto no solo com um ângulo de depressão teta e, de um andar que corresponde à metade da altura desse edifício, observa-se o mesmo objeto com um ângulo de depressão beta. Sabendo que teta e beta são complementares, determine o valor da tangente de teta.

A) √2/2
B) √3/2
C) √2
D) 2√2
E) 3√2

Resposta:

Imagem:

por **Elcioschin** Dom Fev 21 2016, 16:38

Sejam O o ponto ode está o objeto, A o ponto do ângulo θ , E o ponto do ângulo C e P o ponto abaixo de A e E

Seja OP = d

tg(90º - θ) = OP/AP ---> cotgθ = d/H ---> d = H.cotgθ ---> I

tg(90º - β) = OP/EP --> cotgβ = d/(H/2) ---> d = (H/2).cotgβ ---> II

I = II = H.cotgθ = (H/2).cotgβ ---> cotgβ = 2.cotgθ ---> III

θ + β = 90º ---> cotgβ = tgθ ---> IV

IV em III ---> tgθ = 2/tgθ ---> tg²θ = 2 ---> tgθ = √2

por gdo7701 Dom Fev 21 2016, 17:34

Elcioschin escreveu:Sejam O o ponto ode está o objeto, A o ponto do ângulo θ , E o ponto do ângulo C e P o ponto abaixo de A e E

Seja OP = d

tg(90º - θ) = OP/AP ---> cotgθ = d/H ---> d = H.cotgθ ---> I

tg(90º - β) = OP/EP --> cotgβ = d/(H/2) ---> d = (H/2).cotgβ ---> II

I = II = H.cotgθ = (H/2).cotgβ ---> cotgβ = 2.cotgθ ---> III

θ + β = 90º ---> cotgβ = tgθ ---> IV

IV em III ---> tgθ = 2/tgθ ---> tg²θ = 2 ---> tgθ = √2

Perfeito! Muito obrigado amigo! Questão resolvida.

por Conteúdo patrocinado

Questão Trigonometria

Questão Trigonometria

Re: Questão Trigonometria

Re: Questão Trigonometria

Re: Questão Trigonometria

Um fórum livre e democrático.