Valores para constante

x³ - 3x² >/ k ( 3x² - 12x - 4)

Encontre o intervalo de valores que torna a expressão acima verdadeira para todos x>/ 0

Assuma k > 0

Poderiam me ajudar nessa questão?

Vamos, primeiro, tentar identificar as posições relativas entre as duas curvas:

1- na parábola

1.1) o vértice tem coordenadas V(x_v,\;ky_v), ou seja, a constante não altera o eixo de simetria, mas altera a altura do vértice. Nessa parábola o vértice será V(2,\;-16k)

porque:

1.2) para x=0, y=-4k

2- na curva do terceiro grau

1.1) há um máximo em x=0 e um mínimo em x=2.

1.2) o mínimo é (2, -4)

O mínimo da curva do terceiro grau e o vértice (mínimo) da parábola estão na mesma vertical. A parábola é "mais larga" do que a curva do terceiro grau:



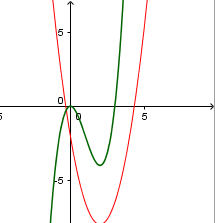
O mais alto que a parábola pode estar é quando seu vértice coincidir com o mínimo da outra curva, ou seja: -16k=-4\;\to\;k=\frac{1}{4}

consequentemente teremos k\geq\frac{1}{4}

Acho que é isso.

Sr. Euclides, também segui um raciocínio observando os gráficos e o fato de a curva do 3° grau aparentar crescer mais rápido do que a do segundo grau!!

Porém, substitui  x= 5 na equação original:

125 - 75>/ k( 75 - 60 - 4)

50 >/ 11 k 

k
Daí, percebi que existe uma condição da seguinte forma:

1/4<\ k <\ n

Não encontrei o n...

Não há restrição para qualquer valor maior que 1/4.

Euclides escreveu:Não há restrição para qualquer valor maior que 1/4.

Mas se k = 5, teremos a expressão:

x³ - 3x² >/ 5 (3x² - 12x - 4)

x³ - 3x² >/ 15x² - 60x - 20

Isso deveria ser válido para todos os x>/0,

Mas se x = 6:

216 - 108 >/ 540 - 360 - 20
108 >/  120...

Ou seja, ficou falsa...

Além disso, tracei no GeoGebra as duas funções, quando k = 5, e percebi que se cruzam em certo ponto, e a partir dali os valores em y da parábola passam a ser maiores que na equação cúbica..

Muito obrigado pela ajuda que está dando Sr. Euclides..
Poderia me esclarecer em que eu estou errando ao afirmar sobre os valores que restringem alguns "k">1/4?


Além disso, poderia avaliar esse outro jeito que eu tentei?


Encontrando os pontos em que a parábola cruza o eixo x:

3kx² - 12kx - 4k = 0


x = [12k+-Raiz quadrada de (144k² + 48k²)]/2.3k


x = [12k +- Raiz quadrada de (192k²)]/6k


x = (12k+- 8.k.√3)/6 = (6k + 4k√3)/3k e (6k - 4k√3)/3k = (6 + 4√3)/3 e (6 - 4√3)/3 --- Não depende de k...


Pensei a partir daí, armar a seguinte:


Desde (6 + 4√3)/3, raiz positiva que nos interessa, a área embaixo do gráfico da equação cúbica tendendo ao infinito deve ser maior do que a área embaixo do gráfico da parábola..


Basicamente: ∫ que vai de (6 + 4√3)/3 até infinito de x³ - 3x² dx>  ∫ que vai de  (6 +4√3)/3 até infinito de  3kx² - 12kx - 4k dx


Integrando a primeira: {[(x^4)/ 4] - x^3} = If(x)


Integrando a segunda: [kx³ - 6kx² - 4kx] = Ig(x)


Se substituirmos no lugar do x o valor ∞, teremos um resultado também de ∞,  assim, basicamente temos:


∞ - If((6 +4√3)/3) >/ ∞ - Ig((6 +4√3)/3))


Ou seja: Ig((6 +4√3)/3))>/ If((6 +4√3)/3)


[k(6 +4√3)/3)³ - 6k(6 +4√3)/3)² - 4k(6 +4√3)/3)]>/ {[((6+4√3)/3)^4)/4] - (6 +4√3)/3^3} 


0>/ {[((6+4√3)/3)^4)/4] - x^3} - {[k(6 +4√3)/3)³ - 6k(6 +4√3)/3)² - 4k(6 +4√3)/3)]}


Vou tirar a substituição que eu fiz de x pela raiz para tentar simplificar..


[(x^4)/4 - x³] - {kx³ - 6kx² - 4kx} < 0 

(x^4)/4 - x³ - kx³ + 6kx² + 4kx < 0


x (x³/4 - x² - kx² + 6kx + 4k) < 0


Bem, gostaria de saber se está certo até aqui, pois devo ter feito muitas coisas desnecessárias e desenvolver a expressão acima vai dar um pouco de trabalho... Mas se estiver certo até aqui, basta adquirir uma inequação em função de k e descobrir o intervalo de valores que a questão pede...


Agradeço desde já...

Você está certo no que diz respeito à existência de um limitante superior. Quanto a estabelecê-lo, ainda não encontrei o raciocínio correto.

x³ - 3x² >/ k ( 3x² - 12x - 4)


x³ - 3x² = 3kx² - 12kx - 4k


x³ - 3x² - 3kx² + 12kx + 4k = m(x)


A partir de x>/ 0, essa função não pode ter valores negativos...


m'(x) = 3x² - 6x - 6kx + 12k
Encontrando os pontos max e min relativos, devemos zerar a derivada:
3x² - 6x - 6kx + 12k= 0

x² - 2x - 2kx + 4k = 0


Solução:
Usando Bháskara:
x = [(2+2k)+- Raiz quadrada de 4k² + 8k + 4 - 16k]/2
x = ([2 + 2k)+-(2 - 2k)]/2
x' = 2, x" = 2k


m(2) = 2³ - 3.(2)² - 3k(2)² + 24k + 4k = 16k - 4 >0, k>1/4
m(2k) = 8k³ - 12k² - 12k³ + 24k² + 4k =  - 4k³ + 12k² + 4k>0,
4k(-k² + 3k +  1) >0
-k² + 3k +  1 >/ 0



k² - 3k - 1

Raízes:


k = 3+-Raiz quadrada de (9+4)/2 = (3 +  √13)/2 e (3-  √13)/2


O que nos interessa é a raiz positiva...


1/4 \< k \< (3 +  √13)/2


Correto?