Reta tangente à curva gama

Sejam  e , diferenciáveis com  e  para todo 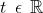. Suponha que a imagem de gama esteja contida na intersecção do gráfico de f com a superfície . Sabendo que (1,0,-1) pertence a imagem de gama, determine uma equação para a reta tangente a gama neste ponto.

RESPOSTA.:X=(1,0,-1) + λ(2,-9,-5)

----------------------------------------------------------------------------------------------------------------------------------------
Eu pensei em calcular o gradiente de g(x)=z^3 + x^3 + yz +x(y^3) no ponto (1,0,-1). Como os dois gradientes são perpendiculares ao vetor tangente à curva, basta fazer o produto vetorial entre os dois gradientes para achar o vetor diretor da reta tangente. O problema é que o resultado foi diferente do gabarito.

Alguém poderia me ajudar?

Eu pensei em uma coisa agora, mas não sei se está correto.
Vou postar a minha resolução abaixo. Se alguém me ajudar postando outra resolução, eu agradeceria.
..................................................................................................
Minha Resolução:

Seja f(x,y)=z:
f(x,y)-z=0

Sendo h(x,y,z)=f(x,y)-z e f(x,y)-z=0 a função h(x,y,z) na superfície de nível 0, temos:


Para , temos:



Como os vetores gradiente são perpendiculares à curva no ponto (1,0,-1), o produto vetorial entre eles dará o vetor tangente. Assim:


Assim, como o vetor diretor é (2,-9,-5) e (1,0,-1) é o ponto de tangência:
X=(1,0,-1) +λ(2,-9,-5)

Novamente, não sei se minha primeira passagem está correta. Se alguém puder me ajudar com outra resolução, eu agradeceria.