Geometria Espacial - Molécula de Metano
3 participantes
Página 1 de 1
 Geometria Espacial - Molécula de Metano
Geometria Espacial - Molécula de Metano
A molécula de metano 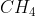 , é constituída de um átomo de carbono, que pode ser considerado como uma esfera situada no centro de um tetraedro regular - ponto de interseção das alturas -, e de quatro átomos esféricos de hidrogênio, cujos centros ocupam os vértices desse tetraedro, conforme ilustra a figura abaixo. Assume-se que os átomos de hidrogênio são tangentes ao de carbono, ou seja, cada um deles toca o átomo de carbono em um único ponto.
, é constituída de um átomo de carbono, que pode ser considerado como uma esfera situada no centro de um tetraedro regular - ponto de interseção das alturas -, e de quatro átomos esféricos de hidrogênio, cujos centros ocupam os vértices desse tetraedro, conforme ilustra a figura abaixo. Assume-se que os átomos de hidrogênio são tangentes ao de carbono, ou seja, cada um deles toca o átomo de carbono em um único ponto.

As quatro ligações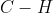 são idênticas, comprimento - distância entre os centros dos átomos - igual a
são idênticas, comprimento - distância entre os centros dos átomos - igual a 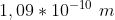 . Sob essas condições e representando por
. Sob essas condições e representando por 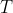 o tetraedro mencionado no texto, julgue os itens abaixo.
o tetraedro mencionado no texto, julgue os itens abaixo.
(1) A altura do tetraedro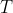 é maior que
é maior que 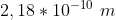 .
.
(2) O triângulo cujos vértices são os centros de dois átomos de hidrogênio e o centro do átomo de carbono é isósceles.
(3) As ligações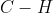 formam entre si ângulos maiores que
formam entre si ângulos maiores que 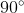 .
.
(4) A distância entre os centros de dois átomos de hidrogênio é maior que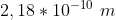 .
.

As quatro ligações
(1) A altura do tetraedro
(2) O triângulo cujos vértices são os centros de dois átomos de hidrogênio e o centro do átomo de carbono é isósceles.
(3) As ligações
(4) A distância entre os centros de dois átomos de hidrogênio é maior que
- Spoiler:
- Obs.: Não tenho gabarito.

ALDRIN- Membro de Honra

- Mensagens : 950
Data de inscrição : 29/07/2009
Idade : 41
Localização : Brasília-DF
 Geometria Espacial - Molécula de Metano
Geometria Espacial - Molécula de Metano
Olá, Aldrin.

R --> raio da esfera maior
r ---> raio das esferas menores
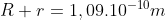
(1)Errado -->
A altura do tetraedro é igual a=2R) .Sendo
.Sendo
) igual a
igual a 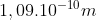 conclui-se que a altura do tetraedro é menor que
conclui-se que a altura do tetraedro é menor que
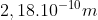
(2) --> Certo
Os centros são equidistantes, logo o triângulo é isósceles.
(3)--> certo
Só seriam formados ângulos de 90º se todas as esferas tivessem o mesmo tamanho.
(4) Errado
Sendo a base um triângulo equilátero, a altura (R-r) do triedro concide com o baricentro do triângulo equilátero,formando um triângulo isósceles de ângulo central igual a 120º e ângulos da base igual a 30º .A base (d) desse triângulo por sua vez será menor (R+r).Logo, a distância será igual ao valor de (d) multiplicado por .
.

R --> raio da esfera maior
r ---> raio das esferas menores
(1)Errado -->
A altura do tetraedro é igual a
(2) --> Certo
Os centros são equidistantes, logo o triângulo é isósceles.
(3)--> certo
Só seriam formados ângulos de 90º se todas as esferas tivessem o mesmo tamanho.
(4) Errado
Sendo a base um triângulo equilátero, a altura (R-r) do triedro concide com o baricentro do triângulo equilátero,formando um triângulo isósceles de ângulo central igual a 120º e ângulos da base igual a 30º .A base (d) desse triângulo por sua vez será menor (R+r).Logo, a distância será igual ao valor de (d) multiplicado por
Última edição por adriano tavares em Ter 23 Nov 2010, 13:53, editado 1 vez(es)
adriano tavares- Grande Mestre

- Mensagens : 600
Data de inscrição : 25/07/2009
Localização : São Paulo
 Tópicos semelhantes
Tópicos semelhantes» Geometria Espacial
» Geometria Espacial
» GEOMETRIA ESPACIAL
» Geometria da molécula - Apolar ou Polar?
» Para determinar a geometria de uma molécula
» Geometria Espacial
» GEOMETRIA ESPACIAL
» Geometria da molécula - Apolar ou Polar?
» Para determinar a geometria de uma molécula
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












