Desigualdades 2
2 participantes
Página 1 de 1
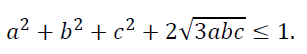
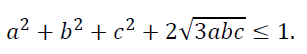
jaques104- Recebeu o sabre de luz
- Mensagens : 149
Data de inscrição : 06/10/2012
Idade : 26
Localização : salvador, BA, Brasil
Re: Desigualdades 2
por ScienceRocks! Dom 19 Jul 2015, 15:22
Lembrando que a²+b²+c²=(a+b+c)²-2(ab+ac+bc), segue que
a^2+b^2+c^2+2\sqrt{3abc}\leq 1\Rightarrow ((1)-2(ab+ac+bc))+2\sqrt{3abc}\leq 1\Rightarrow ab+ac+bc\geq \sqrt{3abc}
Daí,
ab+bc+ac ≥ √(3abc) ⇒ (ab)²+(bc)²+(ac)² ≥ abc(a+b+c), que é valida.
a^2+b^2+c^2+2\sqrt{3abc}\leq 1\Rightarrow ((1)-2(ab+ac+bc))+2\sqrt{3abc}\leq 1\Rightarrow ab+ac+bc\geq \sqrt{3abc}
Daí,
ab+bc+ac ≥ √(3abc) ⇒ (ab)²+(bc)²+(ac)² ≥ abc(a+b+c), que é valida.
ScienceRocks!- Padawan
- Mensagens : 61
Data de inscrição : 19/07/2015
Idade : 28
Localização : Brasil
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
