Marinha - Vetores
2 participantes
Página 1 de 1
 Marinha - Vetores
Marinha - Vetores
Considere B um plano gerado pelos vetores u = i + j - k , e o vetor v = 2i + 3j + 5k e (0,0,1) um ponto de B.
Se B intercepta os eixos coordenados OX, OY, OZ respectivamente nos pontos P=(a,0,0) , Q=(0,b,0) e R=(0,0,c).
Então o valor da soma de a+b+c, vale?
R: 55/56
Se B intercepta os eixos coordenados OX, OY, OZ respectivamente nos pontos P=(a,0,0) , Q=(0,b,0) e R=(0,0,c).
Então o valor da soma de a+b+c, vale?
R: 55/56
raphastars- Iniciante
- Mensagens : 5
Data de inscrição : 26/03/2014
Idade : 37
Localização : Taubaté
 Re: Marinha - Vetores
Re: Marinha - Vetores
Como o plano é gerado pelos vetores u e v, então isso nos diz que os dois vetores pertencem ao plano. Portanto, se fizermos o produto vetorial deles acharemos um novo vetor que será perpendicular tanto a u quando a v, ou seja, é um vetor normal ao plano.
Sabemos também que para determinarmos um plano basta termos o vetor normal ao plano e um ponto desse plano, então iremos calcular esse nosso vetor normal ao plano.
Fazendo o produto escalar de u com v temos:
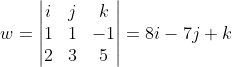 , que esse w é normal ao plano procurado.
, que esse w é normal ao plano procurado.
Assim, temos que a equação do plano será:
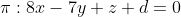
Sabendo que o ponto (0,0,1) é um ponto do plano, então usaremos ele para determinar esse termo independente "d", ou seja, substituindo o ponto na equação do plano temos:
\in&space;\pi\Rightarrow&space;8(0)-7(0)+1+d=0\Rightarrow&space;d=-1\\\\&space;\therefore&space;\pi:8x-7y+z-1=0)
Agora de posse da equação do plano bem definida, vamos achar as intersecções com os planos coordenados, então fazendo a substituição de cada ponto na equação do plano acharemos os seguintes pontos:
;Q=\left&space;(&space;0,-\frac{1}{7}&space;,0\right&space;);R=\left&space;(&space;0,0,1&space;\right&space;)\\\\&space;\therefore&space;a+b+c=\frac{1}{8}-\frac{1}{7}+1=\frac{55}{56})
Sabemos também que para determinarmos um plano basta termos o vetor normal ao plano e um ponto desse plano, então iremos calcular esse nosso vetor normal ao plano.
Fazendo o produto escalar de u com v temos:
Assim, temos que a equação do plano será:
Sabendo que o ponto (0,0,1) é um ponto do plano, então usaremos ele para determinar esse termo independente "d", ou seja, substituindo o ponto na equação do plano temos:
Agora de posse da equação do plano bem definida, vamos achar as intersecções com os planos coordenados, então fazendo a substituição de cada ponto na equação do plano acharemos os seguintes pontos:
Jader- Matador

- Mensagens : 989
Data de inscrição : 06/03/2012
Idade : 30
Localização : Fortaleza - CE
 Tópicos semelhantes
Tópicos semelhantes» Marinha -- KPS
» Marinha -- Pka
» Prova Marinha
» Marinha - Balanceamento
» marinha --- KPS - solubilidade
» Marinha -- Pka
» Prova Marinha
» Marinha - Balanceamento
» marinha --- KPS - solubilidade
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












