geometria plana: área

por catabluma123 Sáb 28 Mar 2015, 17:51

Relembrando a primeira mensagem :

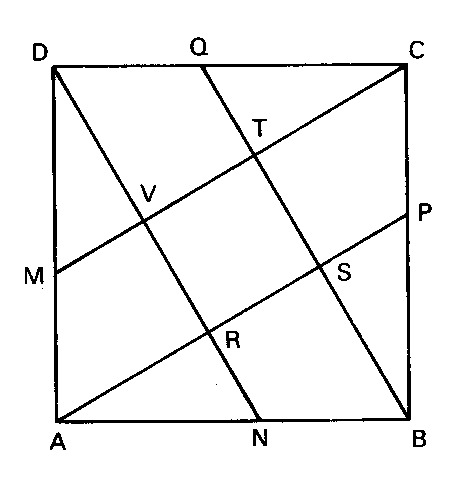
Nessa figura, os pontos M. N. P. Q são pontos médios dos lados do quadrado ABCD, cuja área mede 16 cm2. A área do quadrado RSTV, em cm², mede:

geometria plana: área - Página 2 28v4m0h

geometria plana: área - Página 2 28v4m0h

a)4
b)8
c)10
d)16/3
e)16/5

Gabarito:

por catabluma123 Dom 29 Mar 2015, 18:05

lá vai:

Os pontos P, Q, R e S são pontos médios dos lados de um paralelogramo ABCD de área a².
Qual a área da figura A'B'C'D'?

geometria plana: área - Página 2 14p6ko

gabarito:

por **raimundo pereira** Dom 29 Mar 2015, 19:32

por **Medeiros** Dom 29 Mar 2015, 20:36

catabluma123 escreveu:pelo menos pelo que parece no desenho que tenho aqui na apostila, a área do meio parece que não é um retângulo, apenas um paralelogramo não retângulo

ERRO MEU. Não se pode afirmar que é um retângulo mas pode-se afirmar que é um paralelogramo. E isso não pelo desenho na sua apostila que, pelo menos naqueles que você postou aqui, está distorcido.

por vscarv Sex 28 Set 2018, 15:22

Alguém poderia postar a imagem novamente?

por adriano100 Sex 28 Set 2018, 18:19

O problema original é trivial, e a resposta é 8, há muitas maneiras fáceis de mostrar. Uma delas é por Pitágoras, em que o lado do quadrado interno é a diagonal do triângulo formado por um vértice e os 2 pontos médios mais próximos. Há outros argumentos até mais simples.

Se a questão for de um problema similar, que apareceu na conversa que se seguiu à questão original, mas que não mais mostram a figura comentada, no qual se forma um paralelogramo interno, a partir dos pontos médios e vértices de um paralelogramo externo, veja as respostas no link abaixo:

https://pir2.forumeiros.com/t153190-area-de-quadrilatero-hachurado