Questão Matemática Olímpica

Explique como escrever o número 100 como a soma de parcelas naturais cujo produto sera o maior possível.

O produto é máximo para uma soma fixa quando tiver parcelas iguais. (A interpretação geométrica é que de todos retângulos de mesmo perímetro, o quadrado é o de maior área). A questão inicial é em quanto dividir o número 100.

Dividindo por 2:


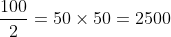
Dividindo em 4 partes iguais:


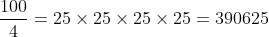
A divisão que dá o maior produto é em partes iguais a  (número de Euler)

Nesse caso o produto máximo ficaria:


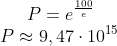
Como a questão exige que as parcelas sejam inteiras, deve-se aproximar o máximo de .




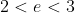
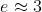
Como 100 não divide 3, o próximo número que divide 3 é 99, mas não serve por 100=99+1 e multiplicar por 1 não aumenta o produto ao máximo, o próximo número é 96. 100=96+4 = 3*32 + 4 = 3*32 + 2*2

Então, para inteiros o produto máximo:


O produto máximo quando os fatores são inteiros é menor que o produto máximo quando os fatores são iguais a .

Pessoal, perdão reviver esse tópico.
Gostaria de saber se alguém consegue me explicar a sugestão de resolução dada pelo Antonio Caminha Muniz, autor da coleção Tópicos de Matemática Elementar.
Ele diz o seguinte: "Se a > 5 é inteiro, mostre que 4(a - 4) > a; conclua, a partir daí, que não é vantajoso termos parcelas maiores que 5. Em seguida, operando trocas semelhantes, descarte parcelas iguais a 4 ou 5. Por fim, mostre, de maneira análoga, que é mais vantajoso termos mais parcelas iguais a 3 que parcelas iguais a 2."

gabriel_balbao escreveu:Pessoal, perdão reviver esse tópico.
Gostaria de saber se alguém consegue me explicar a sugestão de resolução dada pelo Antonio Caminha Muniz, autor da coleção Tópicos de Matemática Elementar.
Ele diz o seguinte: "Se a > 5 é inteiro, mostre que 4(a - 4) > a; conclua, a partir daí, que não é vantajoso termos parcelas maiores que 5. Em seguida, operando trocas semelhantes, descarte parcelas iguais a 4 ou 5. Por fim, mostre, de maneira análoga, que é mais vantajoso termos mais parcelas iguais a 3 que parcelas iguais a 2."

Olá gabriel_balbao;

A ideia do Muniz é algo como o seguinte, imagine uma série de parcelas [latex]a_1 + a_2 + a_3 + ... a_{n-1} + a_n[/latex], com [latex]1 \le n \le 100[/latex] e [latex]\forall i, \text{ } a_i \in \mathbb{N}[/latex]. A análise consiste em verificar se é possível aumentar o produto dessa série de parcelas convertendo uma parcela em outras duas.
Peguemos um valor k, [latex] 1 \le k \le n[/latex], suponhamos a conversão de a_k em duas parcelas b e c (a_k = b+ c).

O produdo da sequência sem a alteração é [latex]a_1 \cdot a_2 \cdot a_3 .... a_{k-1} \cdot (a_k) \cdot a_{k+1} .... a_{n-1} \cdot a_n[/latex]
O produto com alteração é [latex]a_1 \cdot a_2 \cdot a_3 .... a_{k-1} \cdot (b) \cdot (c) \cdot a_{k+1} .... a_{n-1} \cdot a_n[/latex]

Queremos verificar quando que a alteração gera um produto maior, armando a inequação:

[latex]a_1 \cdot a_2 .... a_{k-1} \cdot (b) \cdot (c) \cdot a_{k+1} .... a_{n-1} \cdot a_n > a_1 \cdot a_2 .... a_{k-1} \cdot (a_k) \cdot a_{k+1} .... a_{n-1} \cdot a_n \implies b\cdot c > a_k \implies b \cdot c > b + c \implies 1 > \frac{1}{b} + \frac{1}{c}[/latex]

Como b e c são naturais, os únicos valores que NÃO satisfazem a inequação são:

[latex](b = 1 \text{ e } c \in \mathbb{N} )\text{ ou } (c = 1 \text{ e } b \in \mathbb{N}) \text{ ou } ( b =2 \text{ e } c =2 )[/latex]

Conclusão: Os únicos naturais que NÃO podem ser divididos em duas parcelas que gerem um produto maior são o 2( única parcela possível: 1+1),3 (única parcela possívei 1+ 2)e 4(únicas parcelas possíveis: 1 + 3; 2 +2) então o produto máximo é formado por termos de 2, 3 e 4.

Mas o Muniz segue uma outra linha de raciocínio, ao invés de trabalhar diretamente com a inequação genérica [latex] 1 > \frac{1}{b} + \frac{1}{c} \Leftrightarrow b \cdot c > b + c[/latex] ele faz testagem de valores com o intuito de chegar nas mesmas soluções citadas acima. Ele pede para mostrar que se você pega uma parcela a_k> 5 e converte ela em duas parcelas 4 e (a_k -4) o produto aumenta, demonstração: [latex](a_k - 4)\cdot 4 > ((a_k -4 ) + 4) \implies a_k \ge 6>16/3> 5[/latex]. Pode-se trocar parcelas de 5 por uma de 2 e uma de 3 ,pois o produto aumenta. Demonstração:[latex]3 \cdot 2> 5[/latex]

Aqui o problema se resumiria a dizer que as parcelas são de números menores ou iguais a 4(se for 5 pode-se fazer a troca 2+3 e se for maior que 5 pode-se fazer a troca (a_k -4) + 4), e portanto, as parcelas que maximizam o produto devem ser 1,2, 3 ou 4. O número 1 não pode pois o produto diminui [latex]1\cdot (a_k -1) < a_k[/latex], o 4 pode ser trocado por 2+2 sem efeito observável pois[latex]2 \cdot 2 = 4[/latex]. Ou seja, podemos analisar o problema em termos de parcelas de 2 e 3.

Então a nossa solução pode ser encontrada através de uma soma de α parcelas 2 e β parcelas 3. Logo, 2α + 3β =100 ⇒ β = (100 -2α)/3 e o produto será [latex]2^{\alpha} \cdot 3^\beta = 2^\alpha \cdot 3^{\frac{(100 -2\alpha)}{3}}[/latex].

Deixo por sua conta provar que a função [latex]f(\alpha) = 2^\alpha \cdot 3^{\frac{(100 -2\alpha)}{3}}[/latex] é estritamente decrescente.

O maior valor será a menor solução natural de α em 2α + 3β =100 com β natural ⇒ α=2 e β =32. Lembrando que pode-se fazer a troca de 4 por 2 +2 sem alterar o valor, as soluções pedidas são [latex](2 + 2 + \sum\limits_{i=1}^{\mbox{32}}3) \text{ e } (4 + \sum\limits_{i=1}^{\mbox{32}}3)[/latex].