IME - Geometria Espacial

por frr.soares Sex 20 Fev 2015, 20:29

(IME-RJ) As faces de um paralelepípedo são losangos de lado igual a (raiz quadrada de 2) metros, senda a diagonal menor igual ao lado. O volume desse paralelepípedo vale:

Resposta: 2 m³

por **Medeiros** Sáb 21 Fev 2015, 18:21

As faces deste paralelepípedo são losangos que, devido sua diagonal de mesmo tamanho que o lado, podem ser considerados como dois triângulos equiláteros de lado L=√2 justapostos. Desta forma, os ângulos agudos dos losangos têm 60°. Consequentemente, o vértice agudo do paralelepípedo é formado por três arestas a 60° entre si.

volume: V = S×H,
onde:
S = área da base = área de um losango = área de 2 triângulos equiláteros de lado L
S = 2×L^2 √3/4
S = √3
H = altura do tetraedro de lado L -----> H = L√6/3
.:.
V = √3×√2.√6/3 --------> V = 2 m^3

Se te for preciso, posso postar uma figura.

por **Ashitaka** Sáb 17 Set 2016, 21:57

O problema não é meu, mas agradeço, Medeiros. Não estava enxergando o "tetraedro escondido" e minha altura estava diferente.

por **Medeiros** Sáb 17 Set 2016, 23:39

Ashitaka

Imagine o esqueleto de um cubo com aresta √2 e articulado nos vértices. Comprima-o no plano xOz até a base e o topo ficarem com uma diagonal menor igual à aresta, obviamente que "esticarão" no plano yOz. Depois, mantendo a base fixa no chão, empurre o vértice do topo no sentido da seta vermelha até ajeitar as diagonais das faces laterais igual às arestas. Feito esta deformação, obtemos o paralelepípedo proposto, cujas faces opostas mantém o paralelismo do cubo.

Tentei fazer o desenho. Note que todas as diagonais menores têm mesma medida das arestas. Perceba que as diagonais em azul separam um tetraedro regular de aresta √2 à esquerda, onde calculamos a altura h.

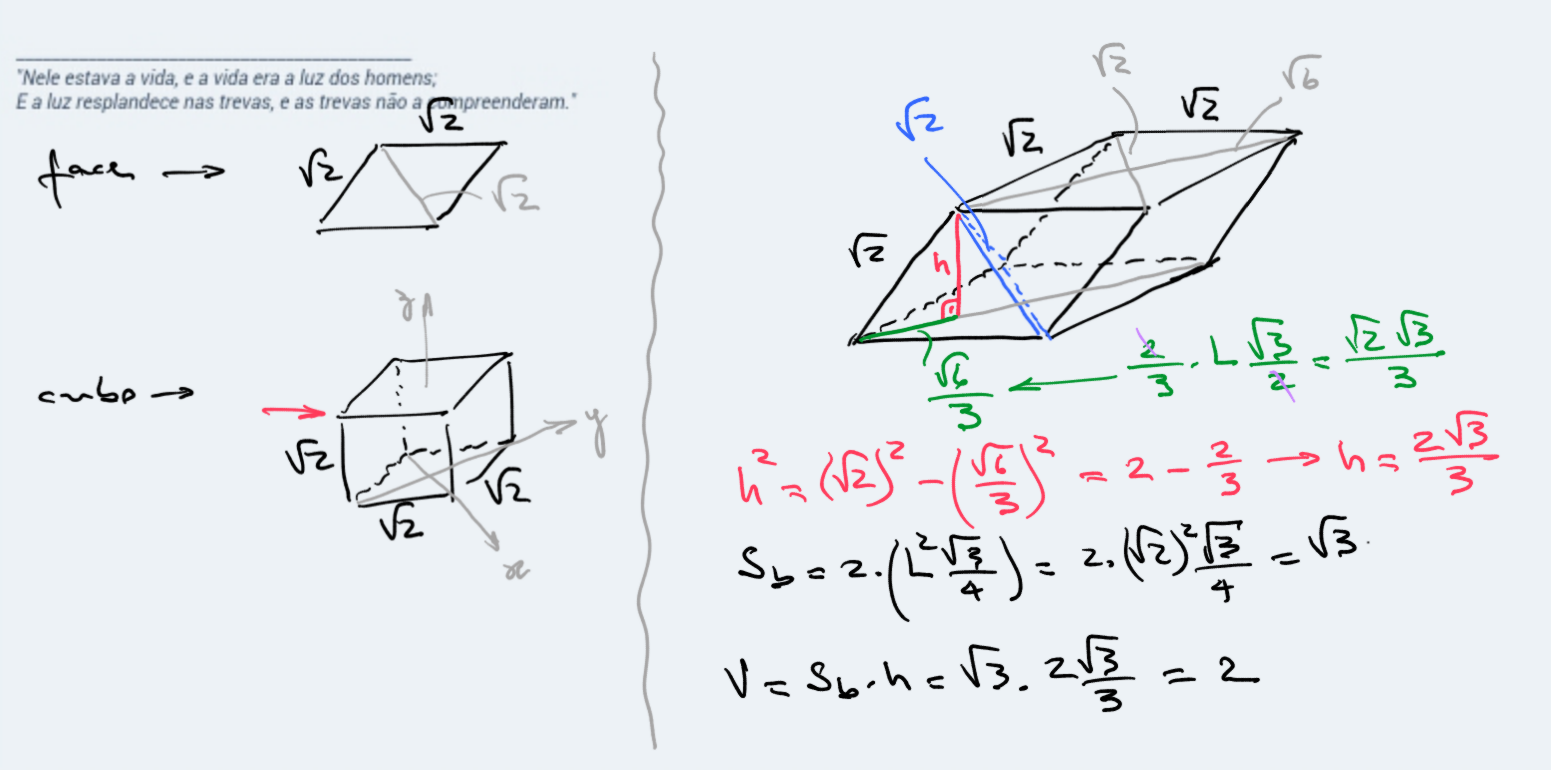
IME - Geometria Espacial 161b7o9

por **Ashitaka** Dom 18 Set 2016, 07:29

Eu já usei essa tática de sucessivas distorções antes, mas não tinha me ocorrido nesse caso. Bem pensado! Eu já havia conseguido imaginar, e assim resolvi com base na sua descrição, mas não desenhar o sólido. Vendo agora, fico fácil de saber desenhar. Obrigado Very Happy