probabilidade de aniversário no mesmo dia
3 participantes
Página 1 de 1
probabilidade de aniversário no mesmo dia
por jubspii Ter 21 Out 2014, 15:44
A Familía do Senhor Koltron é constituido de 10 pessoas; ele e sua esposa, a senhora Doltran e seus oito filhos.
Certa vez, na comemoração de aniversário do seu filho mias novo foram surpreeendidos pela seguinte pergunta:
pai, mãe, qual a probabilidade de que dois de nós, filhos, pelo menos aniversariemos no mesmo dia? O casal parou, pensou e com auxilio de uma calculadora depois de alguns minutos respondeu:
A) 7,42%
B)7,43%
C)8,45%
D)8,46%
E)10,8%
Certa vez, na comemoração de aniversário do seu filho mias novo foram surpreeendidos pela seguinte pergunta:
pai, mãe, qual a probabilidade de que dois de nós, filhos, pelo menos aniversariemos no mesmo dia? O casal parou, pensou e com auxilio de uma calculadora depois de alguns minutos respondeu:
A) 7,42%
B)7,43%
C)8,45%
D)8,46%
E)10,8%
jubspii- Recebeu o sabre de luz
- Mensagens : 100
Data de inscrição : 08/04/2014
Idade : 27
Localização : recife
Re: probabilidade de aniversário no mesmo dia
por Carlos Adir Ter 21 Out 2014, 17:58
Podemos fazer o seguinte: Qual a probabilidade de não fazerem aniversário no mesmo dia?
Ora, se temos o primeiro em um dia, então para o segundo há 364 dias para fazer.
O terceiro, há 363 dias para fazer, e assim por diante. Logo:
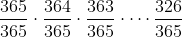
Ou seja:
!}}{365^{10}}=&space;\dfrac{A_{365,10}}{365^{10}} "\dfrac{\dfrac{365!}{(365-10)!}}{365^{10}}= \dfrac{A_{365,10}}{365^{10}}")
O que dá aproximadamente:
p~88,3%
Então a probabilidade de fazer, equivale a 11,7%. Letra E
Ora, se temos o primeiro em um dia, então para o segundo há 364 dias para fazer.
O terceiro, há 363 dias para fazer, e assim por diante. Logo:
Ou seja:
O que dá aproximadamente:
p~88,3%
Então a probabilidade de fazer, equivale a 11,7%. Letra E
____________________________________________
← → ↛ 
⇌ ⇔ ⇐ ⇒ ⇏ ➥
⇌ ⇔ ⇐ ⇒ ⇏ ➥⁰ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ⁺ ⁻ ⁼ ⁽ ⁾ º ª ⁿ ⁱ
₀ ₁ ₂ ₃ ₄ ₅ ₆ ₇ ₈ ₉ ₊ ₋ ₌ ₍ ₎ ₐ ₑ ₒ ₓ ₔ
∴ ≈ ≠ ≡ ≢ ≤ ≥ × ± ∓ ∑ ∏ √ ∛ ∜ ∝ ∞
∀ ∃ ∈ ∉ ⊂ ⊄ ⋂ ⋃ ∧ ∨ ℝ ℕ ℚ ℤ ℂ
⊥ ║ ∡ ∠ ∢ ⊿ △ □ ▭ ◊ ○ ∆ ◦ ⊙ ⊗ ◈
Αα Ββ Γγ Δδ Εε Ζζ Ηη Θθ Ιι Κκ Λλ Μμ Νν Ξξ Οο Ππ Ρρ Σσς Ττ Υυ Φφ Χχ Ψψ Ωω ϑ ϒ ϖ ƒ ij ℓ
∫ ∬ ∭ ∳ ∂ ∇
ℛ ℜ ℰ ℳ ℊ ℒ
Carlos Adir- Monitor
- Mensagens : 2820
Data de inscrição : 27/08/2014
Idade : 28
Localização : Gurupi - TO - Brasil
Re: probabilidade de aniversário no mesmo dia
por PedroCunha Ter 21 Out 2014, 18:11
Carlos, são só os filhos que devem ser considerados.
\frac{365}{365} \cdot \frac{364}{365} \dots \frac{357}{365} = \frac{A_{365,8}}{365^8} \approx 92,57\%
Assim, a probabilidade pedida é 7,43%.
Concorda?
Att.,
Pedro
Assim, a probabilidade pedida é 7,43%.
Concorda?
Att.,
Pedro
PedroCunha- Monitor
- Mensagens : 4639
Data de inscrição : 13/05/2013
Idade : 28
Localização : Viçosa, MG, Brasil
Tópicos semelhantes» [UnB] O Aniversário e a Probabilidade
» Probabilidade - (aniversário)
» PROBABILIDADE DE ANIVERSÁRIO
» Probabilidade e aniversário
» Probabilidade - (festa de aniversário)
» Probabilidade - (aniversário)
» PROBABILIDADE DE ANIVERSÁRIO
» Probabilidade e aniversário
» Probabilidade - (festa de aniversário)
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
