poliedros convexos

por **boris benjamim de paula** Sex 23 Jul 2010, 17:15

Um poliedro convexo possui 1 ângulo pentaédrico, 10 ângulos tetraédricos, e os demais triedros.sabendo que o poliedro tem: número de faces triangulares igual ao número de faces quadrangulares, 11 faces pentagonais, e no total 21 faces, calcule o número de vértices do poliedro convexo.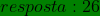 $\bg_green resposta:26$

por cris1995 Dom 18 Out 2015, 13:10

V = 1 + 10 +n

Ft=faces triangulares
Fq=faces quadrangulares
Fp=faces pentagonais=11

Ft+Fq+Fp=21
Ft+Ft+11=21
2Ft=10
Ft=5
Fq=5

2A=1X5+10X4+nx3
2A=5+40+3n
2A=45+3n
A=45/2 +3/2n

V-A+F=2
(11+n)-45/2-3/2n+21=2
n=15

V=11+n=11+15=26

por luizfontes Sex 18 Ago 2017, 20:47

cris1995 escreveu:V = 1 + 10 +n

Ft=faces triangulares
Fq=faces quadrangulares
Fp=faces pentagonais=11

Ft+Fq+Fp=21
Ft+Ft+11=21
2Ft=10
Ft=5
Fq=5

2A=1X5+10X4+nx3
2A=5+40+3n
2A=45+3n
A=45/2 +3/2n

V-A+F=2
(11+n)-45/2-3/2n+21=2
n=15

V=11+n=11+15=26

Olá, desculpa ''ressuscitar'' o tópico, mas alguém poderia me explicar o conceito de ângulo tetraédrico, pentaédrico...

Também não entendi a parte em negrito da resolução.

por Victor Luz Ter 09 Jan 2018, 18:47

Montei a resolução dessa maneira. Apesar de eu não ter usado as primeiras informações do enunciado, cheguei no mesmo resultado. Está correto desenvolver a partir desse modo?

F3= Faces triangulares
F4= Faces quadrangulares
F5= Faces Pentagonais

Pelo enunciado: F3=F4, F=21 e F5= 11

Então, F=F3+F4+F5

21=F3+F4+11

substuindo F4 por F3:

21=2.F3+11

F3=F4=5

Lembrando que Aresta= (n)(F3)+(n)(F4)+n(F5)/2

Onde (n)= número de faces de acordo com o nome, então:

A=3.5+4.5+5.11/2
A=45

Então, pela relação de Euler: V+F=A+2

V=A+2-F
V=45+2-21
V=26

por Conteúdo patrocinado

poliedros convexos

poliedros convexos

Re: poliedros convexos

Re: poliedros convexos

Re: poliedros convexos

Re: poliedros convexos

Um fórum livre e democrático.