conjunto solução de | 9 - 2x| >= |4x|

| 9 - 2x| >= |4x|, qual é o conjunto solução?

Olá fagnerpulca

Lembre-se : |x| = x , se  x ≥ 0
                  |x| = -x , se x < 0

| 9 - 2x| ≥ |4x|  ⇒  | -2x +9 | - |4x| ≥ 0 





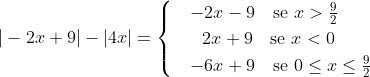
Se x>9/2 , a expressão | -2x +9 | - |4x| é equivalente a -2x-9. Se -2x-9≥0 e  x>9/2 , então x será solução.
-2x -9 ≥ 0  ⇒  x ≤ -9/2 . Não é solução.
Se x>0 , a expressão | -2x +9 | - |4x| é equivalente a 2x+9. Se 2x+9≥0 e  x<0 , então x será solução.
2x+9 ≥ 0  ⇒   x ≥ -9/2  . Logo -9/2 ≤ x < 0 É solução.
Se 0≤x≤9/2 , a expressão | -2x +9 | - |4x| é equivalente a -6x+9 . Se -6x+9≥0  e  0≤x≤9/2  , então x será solução.
-6x+9 ≥  0 ⇒    x ≤ 3/2 .... Logo 0≤ x ≤ 3/2 é solução.

Fazendo a união das soluções:  -9/2 < x < 0 U 0≤ x ≤ 3/2 ⇒  -9/2 ≤ x ≤ 3/2 



Um abraço.

EDIT : O meu erro foi analisar -2x+9 como sendo uma função crescente. Já editei. Obrigado Élcio.

Tem sim, esse é a resposta [-9/2, 3/2]

O modo mais fácil de entender é fazendo o gráfico das duas funções

1) y = |9 - 2x| ---> x = 9/2 ---> y = 0

O gráfico é uma letra V com vértice em V(9/2, 0), com o lado / passando por A(9, 9) e com o lado \ passando por B(0, 9)

2) y - |4x|  ---> x = 0 ---> y = 0

O gráfico é outra letra V com vértice em O(0, 0), com o lado / passando por C(1, 4) e com o lado \ passando por D(-1, 4)

O ponto P de encontro dos dois gráficos à esquerda da origem é dado por: 9 - 2x = - 4x --->  x = - 9/2

O ponto Q de encontro dos dois gráficos à direita da origem é dado por: 9 - 2x = 4x --->  x = 3/2

O gráfico de |9 - 2x| está acima de |4x| apenas no intervalo - 9/2 < x < 3/2